スポンサードリンク
こんにちは、ももやまです。
今回は行列式についてまとめました。少しボリュームが多い記事となってしまったのでゆっくり見てください!
行列式とはどんなものなのか、行列式の計算の仕方、基本変形の種類、覚えていたら便利な行列式の性質、行列式の応用(外積の計算、行列式を用いた階数の判定、固有値算出)を載せています。
前回の余因子編はこちら!(余因子展開で必ず使うので余因子がわかっていない人はこちらを見てください)
スポンサードリンク
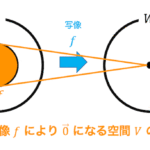
1.行列式のイメージ
行列式のイメージは様々なのですが、私はベクトルが張る面積や体積というイメージを持っています。例えば次の2本のベクトルが張る面積を考えてみましょう。
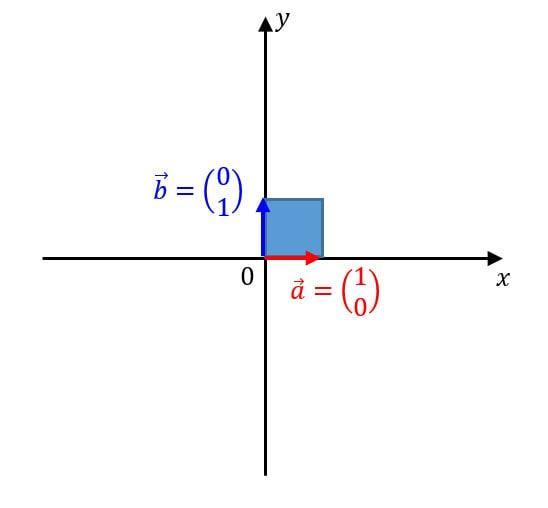
ベクトル*1 \( \vec{a} \) と \( \vec{b} \) が張る青色の図形の面積は1だというのがわかりますね。これが基準の図形になります。これを行列式で表すと、\[ A = \left| \begin{array}{cc} \vec{a} & \vec {b} \end{array} \right| = \left| \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right| \]となりますね。確かに計算すると1になります。これを基準にして他の場合についても考えてみましょう。
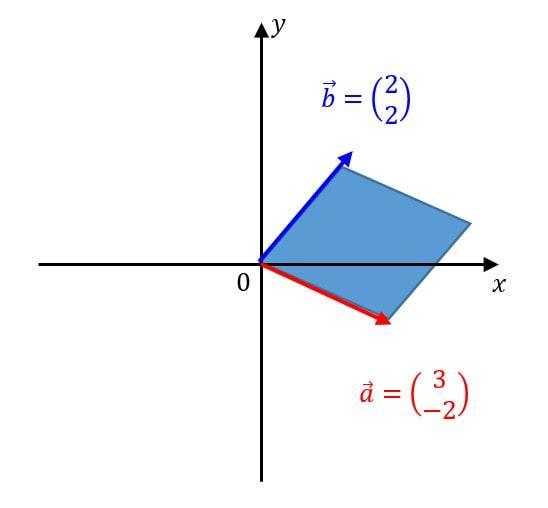
ベクトル \( \vec{a} \) と \( \vec{b} \) を動かすと平行四辺形の面積も当然変わってきます。この場合の面積は、\[ A = \left| \begin{array}{cc} \vec{a} & \vec {b} \end{array} \right| = \left| \begin{array}{cc} 3 & -2 \\ 2 & 2 \end{array} \right| = 6 + 4 = 10 \]ですね。つまり、最初の基準の図形の10倍の面積があるということです。
また、このようなベクトルの配置も考えられます。
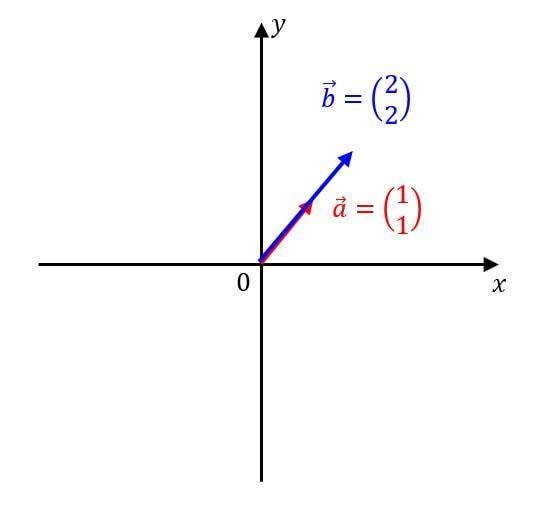
この場合、2本のベクトルの配置からして平行四辺形がまったく出てきませんね。行列式にした場合でも、\[ A = \left| \begin{array}{cc} \vec{a} & \vec {b} \end{array} \right| = \left| \begin{array}{cc} 1 & 2 \\ 1 & 2 \end{array} \right| = 0 \]と、面積が0、つまり平行四辺形が出てこないということがわかります。
しかし、行列式の値は負になることがあります。今まで面積が負の図形なんてありませんでしたよね。このような場合だと行列式が負になります。
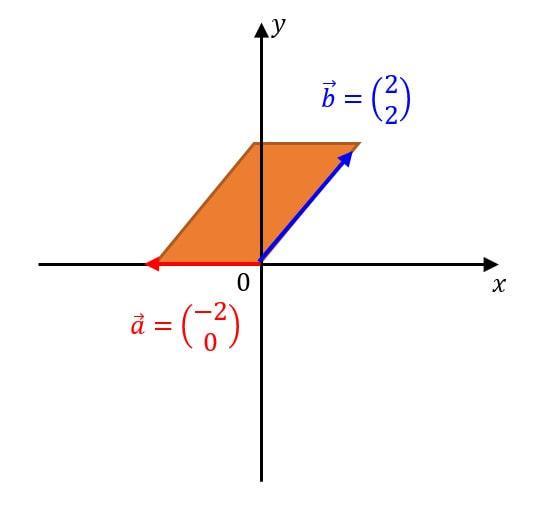
\[ A = \left| \begin{array}{cc} \vec{a} & \vec {b} \end{array} \right| = \left| \begin{array}{cc} -2 & 2 \\ 0 & 2 \end{array} \right| = -4 \]となり、確かに負になります。
図をよく見てみると最初の図形(基準のやつ)と平行四辺形の表裏が逆になっていることがわかります*2。
このように行列式の符号は、図形の表裏を表します。
また、3次元の場合には行列式は、3つのベクトルが張る図形の体積を表します。例えば、このような図形(平行六面体)の体積が計算できます。
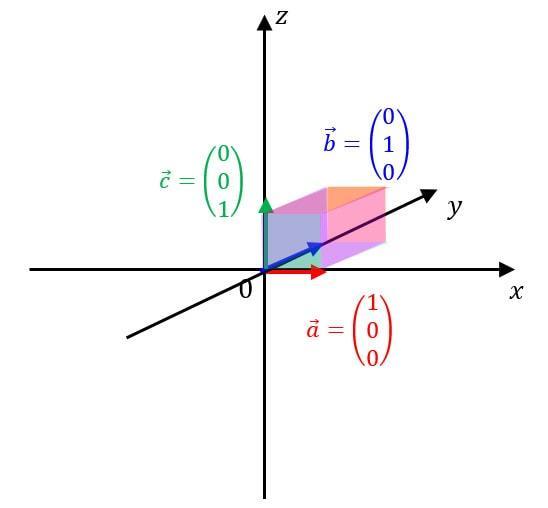
この場合の体積は、\[ A = \left| \begin{array}{cc} \vec{a} & \vec {b} & \vec{c} \end{array} \right| = \left| \begin{array}{cc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0& 1 \end{array} \right| = 1 \]となります。
体積が面積に変わる以外は2次元の場合とすべて同じです。
このように、行列式は、図形の面積や体積の変換の倍率を表すことができるのです。では、実際に行列式はどのようにして計算できるかを順番にまとめていきましょう。
スポンサードリンク
2.サラスの公式
2×2行列、3×3行列の場合、つぎのような公式で行列式を求めることができます。これをサラスの公式といいます。
(1) 2×2行列の行列式
\[
\left| \begin{array}{cc} a & b \\ c & d \end{array} \right| = ad - bc
\]
(2) 3×3行列の行列式
\[
\left| \begin{array}{cc} a & b & c \\ d & e & f \\ g & h & i \end{array} \right| =
aei + bfg + cdh - (ceg + bdi + afh)
\]
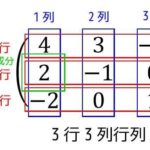
(行列式)=(赤色の矢印方向に掛けた値の和)-(青色の矢印方向に掛けた値の和)
行列の左と右はFFやドラクエの世界地図みたいにつながっていると考えるとわかりやすいです。(灰色でつなげている)
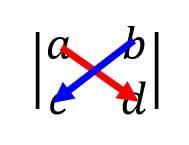
3×3の場合(赤青それぞれ3本ずつ)
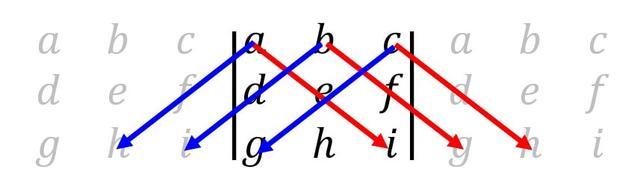
\left| \begin{array}{cc} 1 & 2 \\ 3 & 4 \end{array} \right| = 1 \times 4 - 2 \times 3 = -2 \\
\begin{align*}
& \left| \begin{array}{ccc} 2 & -1 & 3 \\ 3 & 1 & -1 \\ 0 & -3 & 2 \end{array} \right| \\ \ = \ & (2 \times 1 \times 2 + (-1) \times (-1) \times 0 + 3 \times 3 \times (-3) \\ & \ - (3 \times 1 \times 0 + (-1) \times 3 \times 2 + 2 \times (-1) \times (-3)) \\ \ = \ & 4 + 0 - 27 - (0 - 6 + 6) = -23
\end{align*}
\]
スポンサードリンク
3.基本変形
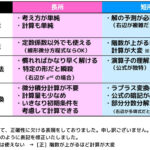
行列式を求める際には、サラスの公式だけでは計算が困難になることが多いです。
そのため、次の3つの法則を使って計算を楽にしてから余因子展開やサラスの公式を使うと計算が楽になります。
余因子展開については下のほうで改めて説明します。
行列式を求める際の変形だけは \( \to \) ではなく \( = \) を使うので要注意!
では、3つのやり方それぞれの説明と、行の変形例と列の変形例の2つを紹介します。
(1) 1行 or 1列を n 倍すると行列式は n 倍になる
このやり方は、行列内の要素に文字が現れたときに役にたちます。文字を外に出すことで行列の中の文字が減ってスッキリします。
例1:1行目の3を外に出す(3で割る)
\[
\begin{align*} &
\left| \begin{array}{ccc} 3_{\div 3} & 3_{\div 3} & 3_{\div 3} \\ 1 & 3 & 2 \\ 2 & 1 & -1 \end{array} \right| \\ \ = & \
3 \left| \begin{array}{ccc} 1 & 1 & 1 \\ 1 & 3 & 2 \\ 2 & 1 & -1 \end{array} \right|
\end{align*}
\] があります。1行目を3で割っていますね。3で割ると、行列式の値は1/3となるため、調整するために3をかけて等式にしています。
例:1列目の3を外に出す(3で割る)
\[
\begin{align*} &
\left| \begin{array}{ccc} 3_{\div 3} & 1 & 4 \\ 3_{\div 3} & -2 & 0 \\ 3_{\div 3} & 3 & 4 \end{array} \right| \\ \ = & \
3 \left| \begin{array}{ccc} 1 & 1 & 4 \\ 1 & -2 & 0 \\ 1 & 3 & 4 \end{array} \right|
\end{align*}
\]
こちらは1列目を3で割っていますね。上と同じように行列式の値は1/3となるため、3をかけて等式になるようにしています。
(2) 2つの行or列を入れ替えると正負が逆転する
2つの行 or 2つの列を入れ替えると正負が入れ替わります。
行の入れ替えの例(1行目と3行目をチェンジ) \[
\left| \begin{array}{ccc} 1 & -1 & 0 \\ 1 & 3 & 2 \\ 2 & 1 & -1 \end{array} \right| = -1
\left| \begin{array}{ccc} 2 & 1 & -1 \\ 1 & 3 & 2 \\ 1 & -1 & 0 \end{array} \right|
\]
列の入れ替えの例(2列目と3列目をチェンジ) \[
\left| \begin{array}{ccc} 1 & -1 & 0 \\ 1 & 3 & 2 \\ 2 & 1 & -1 \end{array} \right| = -1
\left| \begin{array}{ccc} 1 & 0 & -1 \\ 1 & 2 & 3 \\ 2 & -1 & 1 \end{array} \right|
\]
入れ替えの際に-1倍を忘れてしまう人が多いため、私的にはあまり使ってほしくありません。(1)や(3)の変形方法や余因子展開を使って解くやり方をおすすめします。
(3) 1つの行から他の行を何倍かしたものを加えるor引いても行列式は変わらない
3つの中で一番使う行基本変形です。
この(3)の変形と余因子展開を組み合わせ技を使うのが個人的におすすめな行列式の求め方です。
例1:2行目を基準
\[\left| \begin{array}{ccc} 1 & 2 & 2 \\ 0 & 1 & 1 \\ 2_{-2} & -2_{-4} & 1_{-4} \end{array} \right| = \left| \begin{array}{ccc} 1 & 2 & 2 \\ 0 & 1 & 1 \\ 0 & -6 & 3 \end{array} \right| \]
例2:1列目を基準
\[\left| \begin{array}{ccc} 1 & 2_{-2} & 2_{-2} \\ 0 & 1 & 1 \\ 2 & -2_{-4} & 1_{-4} \end{array} \right| = \left| \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 2 & -6 & -3 \end{array} \right| \]
このように、列の1つ以外を0にしてから余因子展開を行うと計算量を少なくして行列式を求めることが可能となります。
(4) 1つの行の値を分割して2つの行列式できる
1つを除いた行もしくは列を固定し、残り1つの行or列を2つで分割することができます。例えば、
\[ \left| \begin{array}{cccc} 3 & 2 & 1 & 2 \\ -2 & 1 & 0 & -1 \\ 1 & -2 & -3 & -2 \\ 6 & 3 & -2 & 5 \end{array} \right|
\]
という行列は例えば以下のように分解できます。
※緑を固定、紫色の行or列を赤色と青色に分解
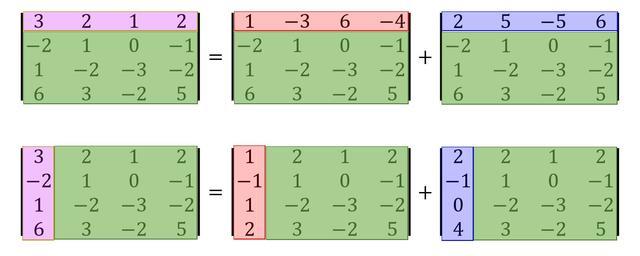
この変形は文字が入っている行列に対して使うことが多いです。例えば、
\[
\begin{align*} &
\left| \begin{array}{ccc} 1 & a & b & c+d \\ 1 & b & c & d+a \\ 1 & c & d & a+b \\ 1 & d & a & b+c \end{array} \right| \\ \ = \ &
\left| \begin{array}{ccc} 1 & a & b & c \\ 1 & b & c & d \\ 1 & c & d & a \\ 1 & d & a & b \end{array} \right| +
\left| \begin{array}{ccc} 1 & a & b & d \\ 1 & b & c & a \\ 1 & c & d & b \\ 1 & d & a & c \end{array} \right|
\end{align*}
\]
と分解できます。*3
4.余因子展開
4×4以上の行列式になると、単にサラスの公式や基本変形だけでは求めることができません。そこで使われるのが余因子展開です。
余因子展開では、1行もしくは1列を選んでそれぞれの要素とその余因子の積をすべて足したものが行列式となります。
具体的に余因子展開の例を1つお見せします。最初にサラスの公式で計算した、\[|A| = \left| \begin{array}{ccc} 2 & -1 & 3 \\ 3 & 1 & -1 \\ 0 & -3 & 2 \end{array} \right| \]を余因子展開しましょう。
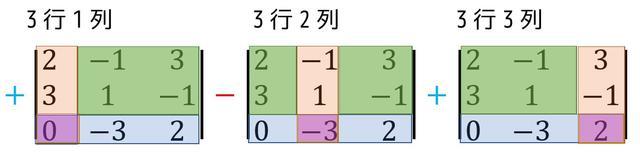
\[
\begin{align*} &
\left| \begin{array}{ccc} 2 & -1 & 3 \\ 3 & 1 & -1 \\ 0 & -3 & 2 \end{array} \right| \\ \ = \ & +
0 \times \left| \begin{array}{ccc} -1 & 3 \\ 1 & -1 \end{array} \right| -
(-3) \times \left| \begin{array}{ccc} 2 & 3 \\ 3 & -1 \end{array} \right| +
2 \times \left| \begin{array}{ccc} 2 & -1 \\ 3 & 1 \end{array} \right| \\ \ = \ &
0 \times (-2) - (-3) \times (-11) + 2 \times 5 \\ \ = \ & -33 + 10 = -23
\end{align*}
\]
と求めることができます。
実際に余因子展開をするときには、事前に基本変形で行や列の中にできる限り0を作ってそれから余因子展開を行うと素早く計算できます。\[
\begin{align*} &
\left| \begin{array}{ccc} 1 & 2 & 2 \\ 0 & 1 & 1 \\ 2_{-2} & -2_{-4} & 1_{-4} \end{array} \right| =
\left| \begin{array}{ccc} 1 & 2 & 2 \\ 0 & 1 & 1 \\ 0 & -6 & -3 \end{array} \right| \\ \ = \ &
1 \left| \begin{array}{ccc} 1 & 1 \\ -6 & -3 \end{array} \right| \\ \ = \ & -3 - (-6) = 3
\end{align*}
\] こんな感じにね。
5.覚えておくと便利な行列式の性質
覚えておくと便利な行列式の性質をいくつかまとめました。
(1) 2つの行列の積の行列式とそれぞれの行列式の積は等しい
数式で表すと、行列 \( A \) と行列 \( B \) があるとき、\[ |A| |B| = |AB| \] が成り立つ。
1つ試してみましょう。
\[ A = \left( \begin{array}{ccc} 1 & 2 \\ 3 & 4 \end{array} \right) , \ \ B = \left( \begin{array}{ccc} -2 & -1 \\ 5 & 4 \end{array} \right)
\\ AB = \left( \begin{array}{ccc} 1 & 2 \\ 3 & 4 \end{array} \right) \left( \begin{array}{ccc} -2 & -1 \\ 5 & 4 \end{array} \right) = \left( \begin{array}{ccc} 8 & 7 \\ 14 & 13 \end{array} \right)
\]
のとき、\[ |A| = 4 - 6 = -2, \ \ |B| = -8 - (-5) = -3, \ \ |AB| = 104 - 98 = 6 = |A||B| \] となって確かに成り立ちますね!
ちなみに2つの行列の和の行列式 \( |A+B| \) とそれぞれの行列式の和 \( |A|+ |B| \) は必ずしも等しくなるとは限りません。
(2) 逆行列の行列式の値はもとの行列の逆数
数式で表すと、行列 \( A \) とその逆行列 \( A^{-1} \) の行列式の関係は、
\[ |A| = \frac{1}{|A^{-1}|} \]
となります。
逆行列や余因子のまとめのページに逆行列の公式を載せているのですが、その公式を見ると、最後に行列式で割っていますよね。詳しくは逆行列のページを見てください。
(3) 行列の行と列を入れ替えても(転置行列)行列式は変化しない
転置行列とは、行と列を入れ替えた行列のことをいいます。
行列 \( A \) の転置行列は \( A^T \) と表されます。
例えば、\[ A = \left( \begin{array}{ccc} 1 & -2 \\ -4 & 5 \end{array} \right) \] とすると、 \[ A^T = \left( \begin{array}{ccc} 1 & -4 \\ -2 & 5 \end{array} \right) \] となります。試しに行列 \( A \) とその転置行列 \( A^T \) の両方の行列式を計算してみてください。確かに一緒になりますよ(行列式はともに-3)。
ちなみに私は検算のためにもとの行列と転置行列を2つ解いて答えが一致するかを確認したりするときに使います。
(4) 上三角行列、下三角行列の行列式は対角成分の積
上三角行列は、対角成分(水色の四角で囲っている)より下がすべて0の行列、下三角行列は対角成分より上がすべて0の行列を表します。そのような行列の行列式は下のようにすべて対角成分をすべて掛けた値となります。

(5) ブロック行列の計算則
行列を同じ大きさ(同じ \( n \) 次正方行列)の行列 \( A,B,C \) と零行列 \( O \) に分解します。このとき、
\[ \left| \begin{array}{ccc} A & B \\ B & A \end{array} \right| = |A+B||A-B|\]
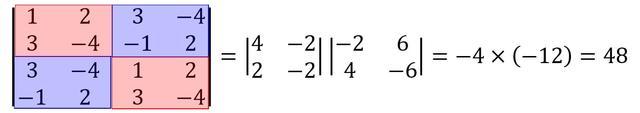
\[ \left| \begin{array}{ccc} A & -B \\ B & A \end{array} \right| = |A+iB||A-iB|\]
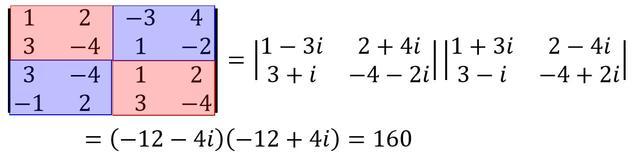
\[ \left| \begin{array}{ccc} A & C \\ O & B \end{array} \right| = |A||B|\]

\[ \left| \begin{array}{ccc} A & O \\ C & B \end{array} \right| = |A||B|\]
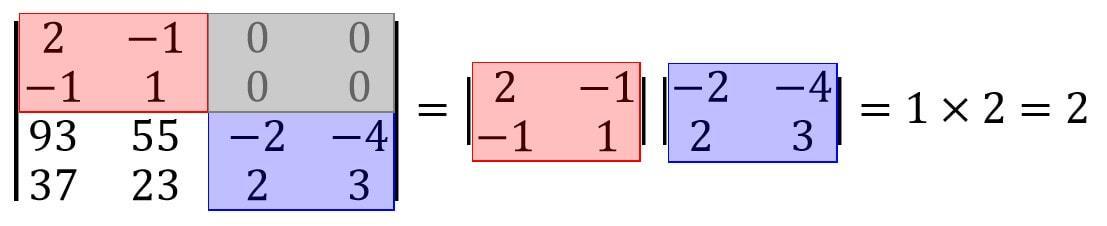
が成立します。*4
6.行列式の応用例
(1) 外積の算出
行列式を使うと外積の公式がわかりやすく表せます。(外積についてはこちらの記事にて解説をしております。)
ベクトル \( \vec{a},\vec{b} \) をそれぞれ\[ \vec{a}= \left( \begin{array}{ccc} a_1 \\ a_2 \\ a_3 \end{array} \right), \ \ \vec{b}= \left( \begin{array}{ccc} b_1 \\ b_2 \\ b_3 \end{array} \right) \]としたときの外積 \( \vec{a} \times \vec{b} \) は、\[ \vec{a} \times \vec{b} =
\left| \begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{array} \right|
\]となります。ただし、\( \vec{i} , \ \vec{j} , \ \vec{k} \) は単位ベクトル\[ \vec{i}= \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right), \ \ \vec{j}= \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \end{array} \right), \ \ \vec{k}= \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \end{array} \right) \]です。上から順番に単位ベクトル、\( \vec{a} \) を横に並べたもの、\( \vec{b} \) を横に並べたものになります。
具体的な数値で1つ例題を出してみましょう。
数検1級の過去問です。
例題1
3つのベクトル \[ \vec{a}= \left( \begin{array}{ccc} 2 \\ 1 \\ -3 \end{array} \right), \ \ \vec{b}= \left( \begin{array}{ccc} 0 \\ -2 \\ 3 \end{array} \right), \ \ \vec{c}= \left( \begin{array}{ccc} 1 \\ -3 \\ 5 \end{array} \right) \] について、
(1) 外積 \( \vec{b} \times \vec{c} \)
(2) 外積 \( \vec{a} \times (\vec{b} \times \vec{c}) \)
を求めなさい。
解答1
\( \vec{i} , \ \vec{j} , \ \vec{k} \) は単位ベクトル\[ \vec{i}= \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right), \ \ \vec{j}= \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \end{array} \right), \ \ \vec{k}= \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \end{array} \right) \]とする。
(1)
\[
\begin{align*}
\vec{b} \times \vec{c} = & \
\left| \begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ 0 & -2 & 3 \\ 1 & -3 & 5 \end{array} \right| \\ = & \ (-10+9)\vec{i} + 3\vec{j} + 2\vec{k} = \left( \begin{array}{ccc} -1 \\ 3 \\ 2 \end{array} \right)
\end{align*}\]
(2)
\[ \begin{align*}
\vec{a} \times (\vec{b} \times \vec{c}) = & \
\left| \begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ 2 & 1 & -3 \\ -1 & 3 & 2 \end{array} \right| \\ = & (2+9)\vec{i} + (3-4)\vec{j} + (6+1)\vec{j} = \left( \begin{array}{ccc} 11 \\ -1 \\ 7 \end{array} \right)
\end{align*} \]
と計算できる。
(2) 階数判定
行列式を用いて階数の判定がある程度できます。
ある \( n \) 次正方行列 \( A \) の行列式が \( |A| \not = 0 \) のときの階数は \( n \) 、それ以外のとき(行列式0)のときは階数が \( n \) 以外であることがわかります。*5
例題2
3次正方行列 \[ \left( \begin{array}{ccc} 2 & 3 & 4 \\ 1 & 2 & 0 \\ 1 & 4 & 1 \end{array} \right)
\] の階数が3になることを確かめなさい。
解説2
サラスだと面白くないので基本変形+余因子展開を使う \[
\begin{align*} &
\left| \begin{array}{ccc} 2_{-2} & 3_{-4} & 4 \\ 1 & 2 & 0 \\ 1_{-1} & 4_{-2} & 1 \end{array} \right| =
\left| \begin{array}{ccc} 0 & -1 & 4 \\ 1 & 2 & 0 \\ 0 & 2 & 1\end{array} \right| \\ \ = \ &
-1 \left| \begin{array}{ccc} -1 & 4 \\ 2 & 1 \end{array} \right| \\ \ = \ & -1(-1 - 8) = 9 \not = 0
\end{align*}
\]より階数が3になることが示された。*6
(3) 固有値算出
行列 \( A \) の対角成分から \( t \) を引いた行列の行列式が0になるときの \( t \) の値を調べることで固有値を算出することができます。
固有値については、また別の機会に詳しくまとめようと思います。
こちらも一応例題を出してみましょう。
例題3
行列 \( A \) と、行列 \( A \) の対角成分から \( t \) を引いた行列 \( B \) を考える。
\[ A = \left( \begin{array}{ccc} 3 & 3 & 7 \\ 8 & -2 & 7 \\ -8 & 8 & -1 \end{array} \right) , \ B = \left( \begin{array}{ccc} 3-t & 3 & 7 \\ 8 & -2-t & 7 \\ -8 & 8 & -1-t \end{array} \right)
\]
(1) \( |B| = 0 \) となる \( t \) の値を3つすべて求めなさい。(固有値)
(2) 求めた3つの \( t \) の積が行列 \( A \) の行列式と等しくなることを確認しなさい。
解答3
(1) 行列 \( B \) をうまく変形してなんとかして文字を行列の外に出していく。
\[
\begin{align*} &
\left| \begin{array}{ccc}3-t & 3 & 7 \\ 8 & -2-t & 7 \\ -8 & 8 & -1-t \end{array} \right| \\ = \ &
\left| \begin{array}{ccc}3-t _{+3}& 3 & 7 \\ 8_{-2-t} & -2-t & 7 \\ -8_{+8} & 8 & -1-t \end{array} \right| \\ = \ &
\left| \begin{array}{ccc} 6-t_{\div (6-t)} & 3 & 7 \\ 6-t_{\div (6-t)} & -2-t & 7 \\ 0 & 8 & -1-t \end{array} \right| \\ = \ &
(6-t) \left| \begin{array}{ccc} 1 & 3 & 7 \\ 1_{-1} & -2-t_{-3} & 7_{-7} \\ 0 & 8 & -1-t \end{array} \right| \\ = \ &
(6-t) \left| \begin{array}{ccc} 1 & 3 & 7 \\ 0 & -5-t_{\div (-5-t)} & 0 \\ 0 & 8 & -1-t \end{array} \right| \\ = \ &
-(6-t)(5+t) \left| \begin{array}{ccc} 1 & 3 & 7 \\ 0 & 1 & 0 \\ 0 & 8 & -1-t \end{array} \right|
\end{align*}
\]
ここまで計算してから余因子展開、
\[
\begin{align*} &
-(6-t)(5+t) \left| \begin{array}{ccc} 1 & 3 & 7 \\ 0 & 1 & 0 \\ 0 & 8 & -1-t \end{array} \right| \\ = & -(6-t)(5+t) \left| \begin{array}{cc} 1 & 0 \\ 8 & -1-t \end{array} \right| \\ = &
(6-t)(t+1)(t+5) = 0
\end{align*}
\]より、\( t = -5,-1,6 \) となる。
(2)
\( A \) の行列式を求める。サラスだと少しきついので基本変形と余因子展開を使う。
\[
\begin{align*} &
\left| \begin{array}{ccc}3 & 3 & 7 \\ 8 & -2 & 7 \\ -8 & 8 & -1 \end{array} \right| \\ = \ &
\left| \begin{array}{ccc}3 & 3 & 7 \\ 8_{-3} & -2_{-3} & 7_{-7} \\ -8 & 8 & -1 \end{array} \right| \\ = \ &
\left| \begin{array}{ccc}3 & 3 & 7 \\ 5_{\div 5} & -5_{\div 5} & 0 \\ -8_{+8} & 8_{-8} & -1 \end{array} \right| \\ = \ &
5 \left| \begin{array}{ccc}3 & 3 & 7 \\ 1 & -1 & 0 \\ 0 & 0 & -1 \end{array} \right| \\ = \ &
-5 \left| \begin{array}{ccc}3 & 3 \\ 1 & -1 \end{array} \right| \\ = \ &
-5 \times (-6) = 30
\end{align*}
\]
となる。\( t \) の3つの値の積は30なので確かに一致する。
7.練習
では何問か練習してみましょう。
問題
つぎの(1)~(5)の行列式をもとめなさい。[(3)は数検1級過去問]
(1) \[ \left| \begin{array}{ccc} 2019 & 2020 \\ 2021 & 2022 \end{array} \right| \] (2) \[ \left| \begin{array}{ccc} 6 & 2 & 4 \\ 5 & 4 & 3 \\ 1 & 6 & 5 \end{array} \right| \] (3) \[ \left| \begin{array}{ccc} 3 & 5 & 7 & 11 \\ 11 & 7 & 5 & 3 \\ 7 & 3 & 11 & 5 \\ 5 & 11 & 3 & 7 \end{array} \right| \] (4) \[ \left| \begin{array}{ccc} 1 & 2 & 4 & 1 & -3 \\ 2 & 1 & -3 & 2 & 2 \\ -2 & 3 & 2 & -3 & 1 \\ 1 & 1 & 1 & 5 & 3 \\ 2 & -1 & 6 & 7 & -3 \end{array} \right| \] (5) \[ \left| \begin{array}{ccc} 1 & x & 1 & y \\ x & 1 & y & 1 \\ 1 & y & 1 & x \\ y & 1 & x & 1 \end{array} \right| \]
解答
(1)
\[
\begin{align*} &
\left| \begin{array}{ccc} 2019 & 2020 \\ 2021_{-2019} & 2022_{-2020} \end{array} \right| \\ = \ &
\left| \begin{array}{ccc} 2019_{-2020} & 2020_{-2020} \\ 2 & 2 \end{array} \right| \\ = \ &
\left| \begin{array}{ccc} -1 & 0 \\ 2 & 2 \end{array} \right| \\ = \ & -2
\end{align*}
\]
(2)
\[
\begin{align*} &
\left| \begin{array}{ccc} 6 & 2 & 4 \\ 5_{-12} & 4_{-4} & 3_{-8} \\ 1_{-18} & 6_{-6} & 5_{-12} \end{array} \right| \\ = \ &
\left| \begin{array}{ccc} 6 & 2 & 4 \\ -7 & 0 & -5 \\ -17 & 0 & -7 \end{array} \right| \\ = \ &
-2 \left| \begin{array}{ccc} -7 & -5 \\ -17 & -7 \end{array} \right| \\ = \ &
-2 \left| \begin{array}{ccc} -7 & -5 \\ -17_{+14} & -7_{+10} \end{array} \right| \\ = \ &
-2 \left| \begin{array}{ccc} -7 & -5 \\ -3 & 3 \end{array} \right| \\ = \ &
-2(-21 -15) = 72
\end{align*}
\]
(3)
\[
\begin{align*} &
\left| \begin{array}{ccc} 3_{11+7+5} & 5_{7+3+11} & 7_{5+11+3} & 11_{3+5+7} \\ 11 & 7 & 5 & 3 \\ 7 & 3 & 11 & 5 \\ 5 & 11 & 3 & 7 \end{array} \right| \\ = \ &
\left| \begin{array}{ccc} 26_{\div 26} & 26_{\div 26} & 26_{\div 26} & 26_{\div 26} \\ 11 & 7 & 5 & 3 \\ 7 & 3 & 11 & 5 \\ 5 & 11 & 3 & 7 \end{array} \right| \\ = \ &
26 \left| \begin{array}{ccc} 1 & 1 & 1 & 1 \\ 11_{-11} & 7_{-11} & 5_{-11} & 3_{-11} \\ 7_{-7} & 3_{-7} & 11_{-7} & 5_{-7} \\ 5_{-5} & 11_{-5} & 3_{-5} & 7_{-5} \end{array} \right| \\ = \ &
26 \left| \begin{array}{ccc} 1 & 1 & 1 & 1 \\ 0 & -4 & -6 & -8 \\ 0 & -4 & 4 & -2 \\ 0 & 6 & -2 & 2 \end{array} \right| \\ = \ &
26 \left| \begin{array}{ccc} -4_{+24} & -6_{-8} & -8_{+8} \\ -4_{+6} & 4_{-2} & -2_{+2} \\ 6 & -2 & 2 \end{array} \right| \\ = \ &
26 \left| \begin{array}{ccc} 20 & -14 & 0 \\ 2 & 2 & 0 \\ 6 & -2 & 2 \end{array} \right| \\ = \ &
52 \left| \begin{array}{ccc} 20_{\div 2} & -14_{\div 2} \\ 2_{\div 2} & 2_{\div 2} \end{array} \right| \\ = \ &
208 \left| \begin{array}{ccc} 10 & -7 \\ 1 & 1 \end{array} \right| \\ = \ &
208(10+7) = 208 \times 17 = 3536
\end{align*}
\]
(4)
\[
\begin{align*} &
\left| \begin{array}{ccc} 1 & 2 & 4 & 1 & -3 \\ 2 & 1 & -3 & 2 & 2 \\ -2 & 3 & 2 & -3 & 1 \\ 1 & 1 & 1 & 5 & 3 \\ 2 & -1 & 6 & 7 & -3 \end{array} \right| \\ = \ &
\left| \begin{array}{ccc} 1 & 2 & 4 & 1 & -3 \\ 2_{-2} & 1_{-4} & -3_{-8} & 2_{-2} & 2_{+6} \\ -2_{+2} & 3_{+4} & 2_{+8} & -3_{+2} & 1_{-6} \\ 1_{-1} & 1_{-2} & 1_{-4} & 5_{-1} & 3_{+3} \\ 2_{-2} & -1_{-4} & 6_{-8} & 7_{-2} & -3_{+6} \end{array} \right| \\ = \ &
\left| \begin{array}{ccc} 1 & 2 & 4 & 1 & -3 \\ 0 & -3 & -11 & 0 & 8 \\ 0 & 7 & 10 & -1 & -5 \\ 0 & -1 & -3 & 4 & 6 \\ 0 & -5 & -2 & 5 & 3 \end{array} \right| \\ = \ &
\left| \begin{array}{ccc} -3 & -11 & 0 & 8 \\ 7 & 10 & -1 & -5 \\ -1 & -3 & 4 & 6 \\ -5 & -2 & 5 & 3 \end{array} \right| \\ = \ &
\left| \begin{array}{ccc} -3_{+3} & -11_{+9} & 0_{-12} & 8_{-18} \\ 7_{-7} & 10_{-21} & -1_{+28} & -5_{+42} \\ -1 & -3 & 4 & 6 \\ -5_{+5} & -2_{+15} & 5_{-20} & 3_{-30} \end{array} \right| \\ = \ &
\left| \begin{array}{ccc} 0 & -2 & -12 & -10 \\ 0 & -11_{+13} & 27_{-15} & 37_{-27} \\ -1 & -3 & 4 & 6 \\ 0 & 13 & -15 & -27 \end{array} \right| \\ = \ &
\left| \begin{array}{ccc} 0 & -2 & -12 & -10 \\ 0 & 2_{-2} & 12_{-12} & 10_{-10} \\ -1 & -3 & 4 & 6 \\ 0 & 13 & -15 & -27 \end{array} \right| \\ = \ &
\left| \begin{array}{ccc} 0 & -2 & -12 & -10 \\ 0 & 0 & 0 & 0 \\ -1 & -3 & 4 & 6 \\ 0 & 13 & -15 & -27 \end{array} \right| \\ = \ & 0
\end{align*}
\]1行が0なので答えは0。
(5)
最初にほかの行をすべて足しこんで \( 2+x+y \) で割るのがおすすめ \[
\begin{align*} &
\left| \begin{array}{ccc} 1 & x & 1 & y \\ x & 1 & y & 1 \\ 1 & y & 1 & x \\ y & 1 & x & 1 \end{array} \right| \\ = \ &
\left| \begin{array}{ccc} 1 & x & 1 & y \\ x & 1 & y & 1 \\ 1 & y & 1 & x \\ y_{1+x+1} & 1 & x & 1 \end{array} \right| \\ = \ &
\left| \begin{array}{ccc} 1 & x & 1 & y \\ x & 1 & y & 1 \\ 1 & y & 1 & x \\ 2+x+y & 2+x+y & 2+x+y & 2+x+y \end{array} \right| \\ = \ &
(2+x+y) \left| \begin{array}{ccc} 1 & x & 1 & y \\ x & 1 & y & 1 \\ 1 & y & 1 & x \\ 1 & 1 & 1 & 1 \end{array} \right| \\ = \ &
(2+x+y) \left| \begin{array}{ccc} 1_{-1} & x_{-y} & 1_{-1} & y_{-x} \\ x & 1 & y & 1 \\ 1 & y & 1 & x \\ 1 & 1 & 1 & 1 \end{array} \right| \\ = \ &
(2+x+y) \left| \begin{array}{ccc} 0 & x-y & 0 & y-x \\ x & 1 & y & 1 \\ 1 & y & 1 & x \\ 1 & 1 & 1 & 1 \end{array} \right| \\ = \ &
(2+x+y)(x-y) \left| \begin{array}{ccc} 0 & 1 & 0 & -1 \\ x_{-y} & 1 & y & 1 \\ 1_{-1} & y & 1 & x \\ 1_{-1} & 1 & 1 & 1 \end{array} \right| \\ = \ &
(2+x+y)(x-y) \left| \begin{array}{ccc} 0 & 1 & 0 & -1 \\ x-y & 1 & y & 1 \\ 0 & y & 1 & x \\ 0 & 1 & 1 & 1 \end{array} \right| \\ = \ &
-(2+x+y)(x-y)^2 \left| \begin{array}{ccc} 1 & 0 & -1 \\ y & 1 & x \\ 1_{-y} & 1_{-1} & 1_{-x} \end{array} \right| \\ = \ &
-(2+x+y)(x-y)^2 \left| \begin{array}{ccc} 1 & 0 & -1 \\ y & 1 & x \\ 1-y & 0 & 1-x \end{array} \right| \\ = \ &
-(2+x+y)(x-y)^2 \left| \begin{array}{ccc} 1 & -1 \\ 1-y & 1-x \end{array} \right| \\ = \ &
-(2+x+y)(x-y)^2 (-x-y+2) \\ = \ &
(x-y)^2 (x+y+2)(x+y-2)
\end{align*}
\]
8.さいごに
今回は行列式の概念、行列式の計算方法、基本変形の仕方、覚えていたら便利な行列式の性質、行列式の応用などについてまとめました。
とくに文字が入っている行列式をそのまま計算するとめんどくさいことになるので割り算などをして必ず行列の外に出してから余因子展開なり基本変形なりサラスの公式などをつかうといいと思います。
*1:今回は列ベクトル(縦ベクトル)でやっていますが、行ベクトル(横ベクトル)を使ってもOKです。
*2:図形ではなく、xy座標自体の表裏が入れ替わっているという人もいます。
*3:この行列式を計算すると0になります。余裕ある人は0になることを証明してみましょう。
*4:一番上のやつは、\[\begin{align*} & \left| \begin{array}{ccc} A & B \\ B & A \end{array} \right| \\ \ = \ & \left| \begin{array}{ccc} A & B \\ A+B & A+B \end{array} \right| \\ \ = \ & \left| \begin{array}{ccc} A-B & B \\ O & A+B \end{array} \right| \\ \ = \ &|A+B||A-B| \end{align*}
\]で示すことができます。
*5:ちなみに行列式が0、つまり階数が減る行列は逆行列は持ちません。
*6:今回の余因子展開は余因子が1行2列なので番号の合計が3となり奇数になるので-1倍されることに注意
関連広告・スポンサードリンク