うさぎでもわかる線形代数　第06羽　1次独立・1次従属

こんにちは、ももやまです。
今回から再び線形代数についてまとめていきたいと思います。

今回はベクトルの1次独立、1次従属についてです。

 

スポンサードリンク

１．1次結合（線形結合）

1次独立、1次従属の説明をする前に、1次結合の説明をしておきましょう。

線形結合とは、とあるベクトル \( \vec{b} \) をベクトルの組 \( \vec{a_1}, \vec{a_2}, \cdots \) を用いて表したものを表します。

具体的に式で表すと、\[ \vec{b} = c_1 \vec{a_1} + c_2 \vec{a_2} +  \cdots +  c_n \vec{a_n} \]となります。

 

例題1

次のベクトル \( \vec{b} \) を3つのベクトル \( \vec{a_1} \), \( \vec{a_2} \), \( \vec{a_3} \) の1次結合で表しなさい。\[
\vec{a_1} = \left( \begin{array}{ccc} 1 \\ 1 \\ -2   \end{array} \right) \ \ \ 
\vec{a_2} = \left( \begin{array}{ccc} 3 \\ 3 \\ 4   \end{array} \right) \ \ \ 
\vec{a_3} = \left( \begin{array}{ccc} -1 \\ -2 \\ -1   \end{array} \right) \ \ \ 
\vec{b} = \left( \begin{array}{ccc} 4 \\ 1 \\ 3   \end{array} \right) \ \ \ 
\]

 

解説1

\( \vec{b} \) を \( \vec{a_1} \), \( \vec{a_2} \), \( \vec{a_3} \) の一次結合で表すためには、\[ \vec{b} = c_1 \vec{a_1} + c_2 \vec{a_2} + c_3 \vec{a_3} \] となる \( c_1 \), \( c_2 \), \( c_3 \) を求めればよい。これは、\[\left\{ \begin{array}{l} 
\ \ \ \ \  c_1  + 3  c_2  - \ \  c_3   = 4 \\
\ \ \ \ \  c_1  + 3  c_2  - 2 c_3  = 1 \\
-2 c_1  + 4  c_2  - \ \   c_3  = 3 
\end{array}\right. \]の連立方程式を解くのと同じ問題となる。

つまり、\[ \left( \begin{array}{ccc} 1 & 3 & -1 \\ 1 & 3 & -2 \\ -2 & 4 & -1  \end{array} \right) \left( \begin{array}{ccc} c_1 \\ c_2 \\ c_3   \end{array} \right) = \left( \begin{array}{ccc} 4 \\ 1 \\ 3   \end{array} \right) \]を解けばよい。

拡大係数行列を用いて解くと、\[ \begin{align*}  &
\left( \begin{array}{ccc|c} 1 & 3 & -1 & 4 \\ 1_{-1} & 3_{-3} & -2_{+1} & 1_{-4} \\ -2_{+2} & 4_{+6} & -1_{-2} & 3_{+8}
\end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc|c} 1 & 3 & -1_{+1} & 4_{+3} \\ 0 & 0 & -1_{\times (-1)} & -3_{\times (-1)} \\ 0 & 10 & -3_{+3} & 11_{+9} \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc|c} 1 & 3_{-3} & 0 & 7_{-6} \\ 0 & 0 & 1 & 3 \\ 0 & 10_{\div 10} & 0 & 20_{\div 10} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc|c} 1 & 0 & 0 & 1 \\ 0 & 0 & 1 & 3 \\ 0 & 1 & 0 & 2 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc|c} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 2 \\ 0 & 0 & 1 & 3 \end{array} \right)  
\end{align*} \]と変形できるので、\[
\vec{b} = \vec{a_1} + 2 \vec{a_2} + 3 \vec{a_3}
\]となる。

（逆行列を使っても解くことができますが、計算量がかなり多くなってしまうのでおすすめしません。）

 

 

スポンサードリンク

２．1次独立・1次従属

では本題の1次独立、1次従属について説明していこうとおもいます。

\( n \) 本のベクトルの組 \( \vec{a_1}, \vec{a_2}, \cdots, \vec{a_n} \) が\[
c_1 \vec{a_1} + c_2 \vec{a_2} +  \cdots +  c_n \vec{a_n} = \vec{0}
\]を満たす \( c_1, c_2 , \cdots , c_n \) が \[ c_1 = c_2 = \cdots = c_n = 0 \]しかない（すべてが0のとき以外成立しない）とき、ベクトルの組は1次独立（線形独立）であるといいます。

逆に、\( c_1, c_2 , \cdots , c_n \) のうち、1つでも0でないような \( c_1, c_2 , \cdots , c_n \) が存在する（1次独立でない）とき、ベクトルの組は1次従属（線形従属）であるといいます。

1次従属については、ベクトルの組 \( \vec{a_1}, \vec{a_2}, \cdots, \vec{a_n} \) のうちの1つのベクトルを他のベクトルの組で表すことができたら*11次従属ということができる、と言い換えることができます。

 

 

試しに2次元ベクトル、3次元ベクトルで1次独立、1次従属のイメージを見てみましょう。

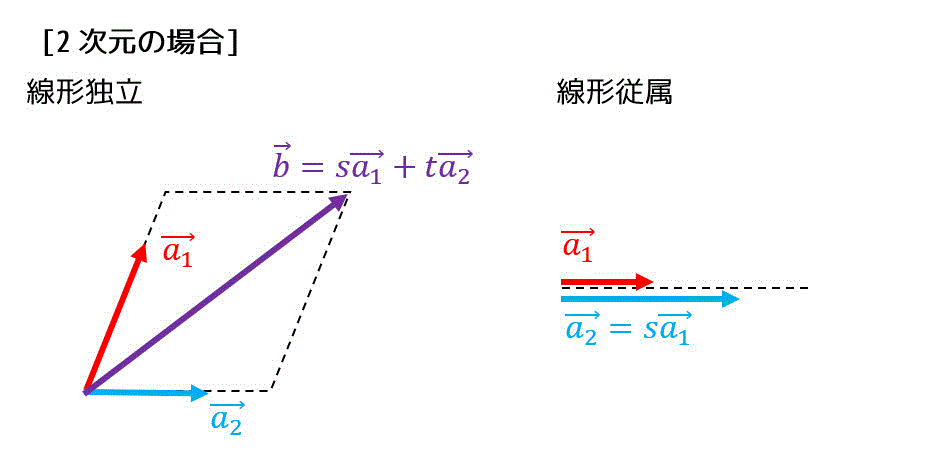
2次元ベクトル（平面ベクトル）の場合

1次独立（線形独立）の場合、2つのベクトル \( \vec{a_1} \), \( \vec{a_2} \) を用いて任意の平面ベクトル \[ \vec{b} = s \vec{a_1} + t \vec{a_2} \]を構成することができます（それぞれの平面ベクトルに対し、\( s,t \) は1通りのみ存在）。

しかし、1次従属（線形従属）の場合、\( \vec{a_2} = s \vec{a_1} \) となる実数 \( s \) が存在するため、\( \vec{a_1} \), \( \vec{a_2} \) は平行となります。

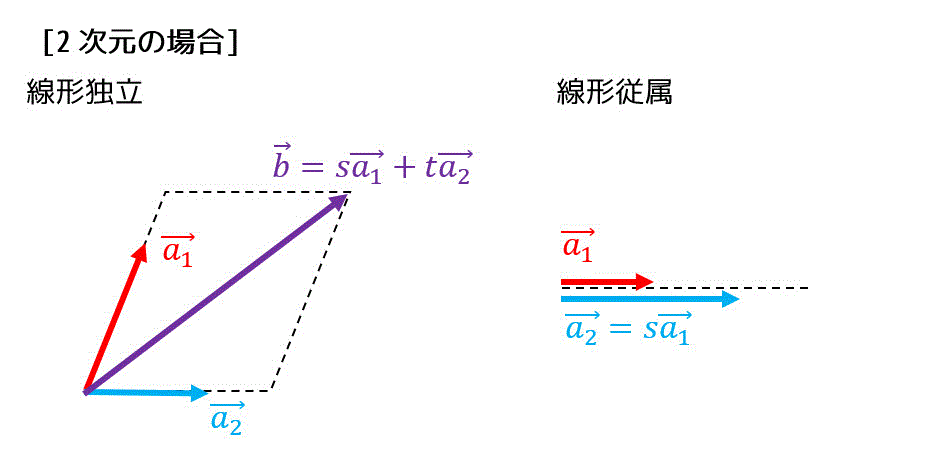
3次元ベクトル（空間ベクトル）の場合

1次独立（線形独立）の場合、2つのベクトル \( \vec{a_1} \), \( \vec{a_2} \), \( \vec{a_3} \) を用いて任意の空間ベクトル \[ \vec{b} = s \vec{a_1} + t \vec{a_2} + u \vec{a_3} \]を構成することができます（それぞれの空間ベクトルに対し、\( s,t,u \) は1通りのみ存在）。

しかし、1次従属（線形従属）の場合、\( \vec{a_3} = s \vec{a_1} + t \vec{a_2} \) となる実数 \( s,t \) が存在するため、空間ベクトルを構成することができず、平面ベクトル、もしくはベクトルの組が互いに平行となります。

 

例題2

3つのベクトルの組 \[
\vec{a_1} = \left( \begin{array}{ccc} 3 \\ 1 \\ 2   \end{array} \right) \ \ \ 
\vec{a_2} = \left( \begin{array}{ccc} 4 \\ 3 \\ 1   \end{array} \right) \ \ \ 
\vec{a_3} = \left( \begin{array}{ccc} 5 \\ 2 \\ 3   \end{array} \right) \ \ \ 
\]は1次独立、1次従属のどちらか。

解説2

\[ c_1 \vec{a_1} + c_2 \vec{a_2} + c_3 \vec{a_3} = \vec{0} \]を満たす \( c_1 \), \( c_2 \), \( c_3 \) はすべて0以外存在しないか、1つでも0でないような組み合わせが存在するかを調べる。

これは、\[\left\{ \begin{array}{l} 
3 c_1  + 4  c_2  + 5  c_3   = 0 \\
\ \  c_1  + 3  c_2  + 2 c_3  = 0 \\
2 c_1  + 1  c_2  + 3  c_3  = 0 
\end{array}\right. \]の連立方程式を解くのと同じ問題となる。

つまり、\[ \left( \begin{array}{ccc} 3 & 4 & 5 \\ 1 & 3 & 2 \\ 2 & 1 & 3  \end{array} \right) \left( \begin{array}{ccc} c_1 \\ c_2 \\ c_3   \end{array} \right) = \left( \begin{array}{ccc} 0 \\ 0 \\ 0   \end{array} \right) \]を解けばよい。\[ \begin{align*}  &
\left( \begin{array}{cccc} 3_{-3} & 4_{-9} & 5_{-6} \\ 1 & 3 & 2 \\ 2_{-2} & 1_{-6} & 3_{-4} \end{array} \right) \\ \to \ & 
\left( \begin{array}{cccc} 0 & -5 & -1 \\ 1 & 3 & 2 \\ 0 & -5_{+5} & -1_{+1} \end{array} \right) \\ \to \ & 
\left( \begin{array}{cccc} 0 & -5_{\times (-1)} & -1_{\times (-1)} \\ 1 & 3_{-10} & 2_{-2} \\ 0 & -5_{+5} & -1_{+1} \end{array} \right) \\ \to \ & 
\left( \begin{array}{cccc} 0 & 5 & 1 \\ 1 & -7 & 0 \\ 0 & 0 & 0 \end{array} \right) \\ \to \ & 
\left( \begin{array}{cccc} 1 & -7 & 0 \\ 0 & 5 & 1 \\ 0 & 0 & 0 \end{array} \right)
\end{align*} \]となる。つまり、\[\left\{ \begin{array}{l} c_1 - 7c_2 = 0 \\ 5c_2 + c_3  \end{array}\right. \]と変形できる。この式を満たす \( c_1 \), \( c_2 \), \( c_3 \) は例えば \( c_1 = 7 \), \( c_2 = 1 \), \( c_3 = -5 \) がある。つまり、\[
7 \vec{a_1} + \vec{a_2} - 5 \vec{a_3} = \vec{0}
\]という関係式が得られるため、1次従属である。

（実際に答案を書く時はいきなり係数行列 \[ A =  \left( \begin{array}{ccc} 3 & 4 & 5 \\ 1 & 3 & 2 \\ 2 & 1 & 3  \end{array} \right) \]を掃き出しを行ってよい。）

 

 

列ベクトルを順番に並べて作成した行列 \( A \) の行基本変形の過程を見てみましょう。

 

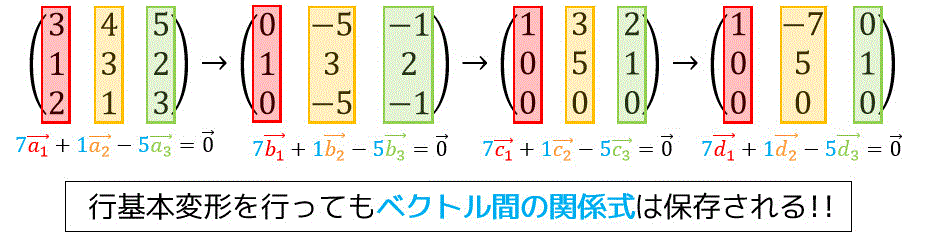
どの行基本変形の段階でも、列ベクトル同士に並ぶベクトル間の関係式は変わってないことがわかりますね。

つまり、行基本変形を行ってもベクトル間の関係式は保存されることがわかります。

 

ベクトル間の関係式が保存することを利用すると、例題2の自明ではない関係式をより素早く算出することができます。

例題2の自明でない関係式の作成法の別解

\[ \begin{align*}  &
\left( \begin{array}{cccc} 3_{-3} & 4_{-9} & 5_{-6} \\ 1 & 3 & 2 \\ 2_{-2} & 1_{-6} & 3_{-4} \end{array} \right) \\ \to \ & 
\left( \begin{array}{cccc} 0 & -5 & -1 \\ 1 & 3 & 2 \\ 0 & -5_{+5} & -1_{+1} \end{array} \right) \\ \to \ & 
\left( \begin{array}{cccc} 0 & -5_{\times (-1)} & -1_{\times (-1)} \\ 1 & 3_{-10} & 2_{-2} \\ 0 & -5_{+5} & -1_{+1} \end{array} \right) \\ \to \ & 
\left( \begin{array}{cccc} 0 & 5 & 1 \\ 1 & -7 & 0 \\ 0 & 0 & 0 \end{array} \right) \\ \to \ & 
\left( \begin{array}{cccc} 1 & -7 & 0 \\ 0 & 5 & 1 \\ 0 & 0 & 0 \end{array} \right)
\end{align*} \]と変形できる。ここで行基本変形後のベクトルをそれぞれ\[
\vec{b_1} = \left( \begin{array}{ccc} 1 \\ 0 \\ 0   \end{array} \right) \ \ \ 
\vec{b_2} = \left( \begin{array}{ccc} -7 \\ 5 \\ 0   \end{array} \right) \ \ \ 
\vec{b_3} = \left( \begin{array}{ccc} 0 \\ 1 \\ 0   \end{array} \right) \ \ \ 
\]とすると、\[ \vec{b_2} = - 7 \vec{b_1} + 5 \vec{b_3} \]が成立する。

行基本変形を施してもベクトル間の関係式は保存されるので、\[
\vec{a_2} = - 7 \vec{a_1} + 5 \vec{a_3} \\ - 7 \vec{a_1} - \vec{a_2} + 5 \vec{a_3} = \vec{0} \]の関係式が成り立ち、1次従属であることがわかる。

 

1次従属、1次独立は行列の階数を用いても判定することができます。

 

例題2を行列の階数を用いて解いてみましょう。

例題3

例題2と同じ3つのベクトルの組 \[
\vec{a_1} = \left( \begin{array}{ccc} 3 \\ 1 \\ 2   \end{array} \right) \ \ \ 
\vec{a_2} = \left( \begin{array}{ccc} 4 \\ 3 \\ 1   \end{array} \right) \ \ \ 
\vec{a_3} = \left( \begin{array}{ccc} 5 \\ 2 \\ 3   \end{array} \right) \ \ \ 
\]は1次独立、1次従属のどちらかを行列の階数を用いて判定しなさい。

解説3

行列 \( A \) を、\[
A = \left( \vec{a_1}, \vec{a_2}, \vec{a_3} \right) = \left( \begin{array}{ccc} 3 & 4 & 5 \\ 1 & 3 & 2 \\ 2 & 1 & 3  \end{array} \right)
\]とすると、\[ \begin{align*}  &
\left( \begin{array}{cccc} 3_{-3} & 4_{-9} & 5_{-6} \\ 1 & 3 & 2 \\ 2_{-2} & 1_{-6} & 3_{-4} \end{array} \right) \\ \to \ & 
\left( \begin{array}{cccc} 0 & -5 & -1 \\ 1 & 3 & 2 \\ 0 & -5_{+5} & -1_{+1} \end{array} \right) \\ \to \ & 
\left( \begin{array}{cccc} 0 & -5 & -1 \\ 1 & 3 & 2 \\ 0 & 0 & 0 \end{array} \right) 
\end{align*} \]となる。

ここで、\[  \mathrm{rank} \ A = 2 < 3 \]となるため、1次従属となる。

 

さらに、行列 \( A \) が正方行列の場合は行列式を用いて判定することもできます。

 

例題4を行列の階数を用いて解いてみましょう。

例題4

例題2と同じ3つのベクトルの組 \[
\vec{a_1} = \left( \begin{array}{ccc} 3 \\ 1 \\ 2   \end{array} \right) \ \ \ 
\vec{a_2} = \left( \begin{array}{ccc} 4 \\ 3 \\ 1   \end{array} \right) \ \ \ 
\vec{a_3} = \left( \begin{array}{ccc} 5 \\ 2 \\ 3   \end{array} \right) \ \ \ 
\]は1次独立、1次従属のどちらかを行列式を用いて判定しなさい。

解説4

行列 \( A \) を、\[
A = \left( \vec{a_1}, \vec{a_2}, \vec{a_3} \right) = \left( \begin{array}{ccc} 3 & 4 & 5 \\ 1 & 3 & 2 \\ 2 & 1 & 3  \end{array} \right)
\]とすると、\[
\begin{align*}  |A| = &
\left| \begin{array}{ccc} 3 & 4 & 5 \\ 1 & 3 & 2 \\ 2 & 1 & 3  \end{array} \right|
\\ = & 27 + 16 + 5 - 30 - 12 - 6
\\ = & 48 - 48 
\\ = & 0
\end{align*}  \]となるので係数行列は正則でない。

よって1次従属となる。

 

その他1次独立、1次従属を使った定理を紹介します。 
余裕があれば頭に入れておきましょう。

 

 

 

 

 

スポンサードリンク

３．1次独立なベクトルの最大数・最大組

ベクトルの組が1次従属であったとしても、ベクトルの組の中からいくつか取り出して新たにベクトルの組を作成すると1次独立になることはありますね。

 

 

 

例題5

つぎに与えられる4つのベクトル \( \vec{a_1} \), \( \vec{a_2} \), \( \vec{a_3} \), \( \vec{a_4} \) の1次独立なベクトルの最大数、最大組を求めなさい。\[
\vec{a_1} = \left( \begin{array}{ccc} 2 \\ 1 \\ 1 \\ 0   \end{array} \right) \ \ \ 
\vec{a_2} = \left( \begin{array}{ccc} 1 \\ 1 \\ 0 \\ 3   \end{array} \right) \ \ \ 
\vec{a_3} = \left( \begin{array}{ccc} 1 \\ 3 \\ 0 \\ 7   \end{array} \right) \ \ \ 
\vec{a_4} = \left( \begin{array}{ccc} 1 \\ 0 \\ 1 \\ -3   \end{array} \right) 
\] 

 

解説5

行基本変形を行ってもベクトル同士に並ぶベクトル間の関係式が変わらないことを利用します。行列 \( A \) を \[ A = \left( \vec{a_1}, \vec{a_2}, \vec{a_3}, \vec{a_4} \right) = 
\left( \begin{array}{ccc} 2 & 1 & 1 & 1 \\ 1 & 1 & 3 & 0 \\ 1 & 0 & 0 & 1 \\ 0 & 3 & 7 & -3  \end{array} \right) \]とします。

行基本変形を行うと、\[
\begin{align*} &
\left( \begin{array}{ccc} 2_{-2} & 1 & 1 & 1_{-2} \\ 1_{-1} & 1 & 3 & 0_{-1} \\ 1 & 0 & 0 & 1 \\ 0 & 3 & 7 & -3  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 0 & 1 & 1 & -1 \\ 0 & 1 & 3 & -1 \\ 1 & 0 & 0 & 1 \\ 0 & 3 & 7 & -3  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1 & 0 & 0 & 1 \\ 0 & 1_{-1} & 3_{-1} & -1_{+1} \\ 0 & 1 & 1 & -1 \\ 0 & 3_{-3} & 7_{-3} & -3_{+3}  \end{array} \right)\\ \to \ & 
\left( \begin{array}{ccc} 1 & 0 & 0 & 1 \\ 0 & 0 & 2 & 0 \\ 0 & 1 & 1 & -1 \\ 0 & 0 & 4_{-4} & 0  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1 & 0 & 0 & 1 \\ 0 & 0 & 2_{\div 2} & 0 \\ 0 & 1 & 1_{-1} & -1 \\ 0 & 0 & 4_{-4} & 0  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 0 & 0  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0  \end{array} \right) 
\end{align*} 
\]と変形できる。

行列 \( A \) の階数が3なので、1次独立なベクトルの最大数が3であることがわかります。

ここで行基本変形後の行列 \( B \) からなるベクトルを\[
B = \left( \vec{b_1}, \vec{b_2}, \vec{b_3}, \vec{b_4} \right)
\]とすると、\[
\vec{b_1} = \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \\ 0   \end{array} \right) \ \ \ 
\vec{b_2} = \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \\ 0   \end{array} \right) \ \ \ 
\vec{b_3} = \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \\ 0   \end{array} \right) \ \ \ 
\vec{b_4} = \left( \begin{array}{ccc} 1 \\ -1 \\ 0 \\ 0   \end{array} \right) 
\] となります。

\( \vec{b_1} \), \( \vec{b_2} \), \( \vec{b_3} \) の組は1次独立であることがわかりますね。しかし、\( \vec{b_4} \) は、\[
\vec{b_4} = \vec{b_1} - \vec{b_2}
\]という１次関係がありますね。なので、\[
\vec{a_4} = \vec{a_1} - \vec{a_2}
\]という１次関係もあり、\( \vec{a_4} \) を加えてしまうと1次従属となってしまいます。よって１次独立なベクトルの最大数は確かに3つあることがわかりますね。

また、最大組は \( \vec{a_1} \), \( \vec{a_2} \), \( \vec{a_3} \) となります。

 

 

最大組を選ぶ際には、わざわざ1次関係を調べなくても、行基本変形後の行列に注目するだけで選ぶことができます。

行列を行基本変形した際の下の0の数に注目し、場合分けを行います。

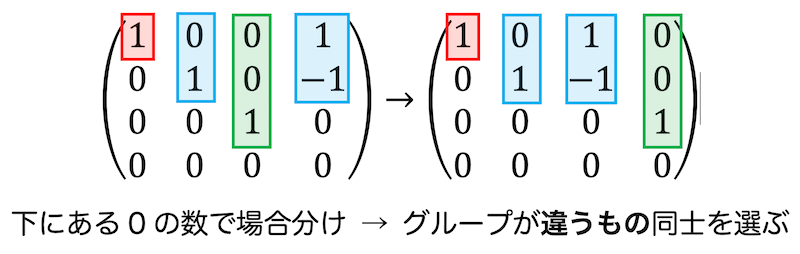
この場合分けのグループが互いに異なるものを最大数だけ選べば、1次関係を調べることなく確実に1次独立の最大組を見分けることができます。

 

４．練習問題

では、実際に何問か練習してみましょう。

練習1

次の3つ、もしくは4つのベクトルの組は1次独立、1次従属のどちらであるか答えなさい。ただし、1次従属であるときは自明ではない関係式を1つ挙げなさい。

(1) \[
\vec{a_1} = \left( \begin{array}{ccc} 1 \\ -1 \\ 2   \end{array} \right) \ \ \ 
\vec{a_2} = \left( \begin{array}{ccc} -2 \\ 1 \\ 0   \end{array} \right) \ \ \ 
\vec{a_3} = \left( \begin{array}{ccc} 4 \\ 2 \\ -1   \end{array} \right) \ \ \ 
\]

(2)  \[
\vec{a_1} = \left( \begin{array}{ccc} 1 \\ 2 \\ 3   \end{array} \right) \ \ \ 
\vec{a_2} = \left( \begin{array}{ccc} -1 \\ 1 \\ 3   \end{array} \right) \ \ \ 
\vec{a_3} = \left( \begin{array}{ccc} 6 \\ 3 \\ 0   \end{array} \right) \ \ \ 
\vec{a_4} = \left( \begin{array}{ccc} 1 \\ 0 \\ -1   \end{array} \right) \ \ \ 
\]

 

練習2

つぎの3本の3次元ベクトルの組が１次従属となるような \( x \) の値を求めなさい。\[
\vec{a_1} = \left( \begin{array}{ccc} 1 \\ 0 \\ 1   \end{array} \right) \ \ \ 
\vec{a_2} = \left( \begin{array}{ccc} 1 \\ 1 \\ x   \end{array} \right) \ \ \ 
\vec{a_3} = \left( \begin{array}{ccc} 2 \\ 1 \\ -1   \end{array} \right) \ \ \ 
\]

（このタイプも試験に頻出します！！）

 

練習3

つぎの5本の4次元ベクトルの組 \( \vec{a_1} \), \( \vec{a_2} \), \( \vec{a_3} \), \( \vec{a_4} \), \( \vec{a_5} \) の線形独立なベクトルの最大数、最大組を求めなさい。

さらに、他のベクトルを最大組の1次結合で表しなさい。\[
\vec{a_1} = \left( \begin{array}{ccc} 0 \\ 3 \\ 1 \\ 1   \end{array} \right) \ \ \ 
\vec{a_2} = \left( \begin{array}{ccc} 1 \\ 0 \\ -2 \\ 1   \end{array} \right) \ \ \ 
\vec{a_3} = \left( \begin{array}{ccc} -1 \\ 1 \\ -4 \\ -2   \end{array} \right) \ \ \ 
\vec{a_4} = \left( \begin{array}{ccc} 0 \\ 7 \\ -4 \\ -1   \end{array} \right) \ \ \
\vec{a_5} = \left( \begin{array}{ccc} 2 \\ 3 \\ -3 \\ -1   \end{array} \right) 
\] 

 

 

５．練習問題の答え

解答1

次の3つ、もしくは4つのベクトルの組は1次独立、1次従属のどちらであるか答えなさい。ただし、1次従属であるときは自明ではない関係式を1つ挙げなさい。

(1) 

行列 \( A \) を\[ A = \left( \vec{a_1}, \vec{a_2}, \vec{a_3}\right) = 
\left( \begin{array}{ccc} 1 & -2 & 4 \\ -1 & 1 & 2 \\ 2 & 0 & -1 \end{array} \right) \]とします。

パターン1　行列の階数で判定する方法

自明でない関係式を1つ答えるような問題では、行基本変形をして求めるのが確実。
行基本変形を行うことで関係式を見つけやすくなる。\[
\begin{align*} &
\left( \begin{array}{ccc} 1 & -2 & 4 \\ -1_{+1} & 1_{-2} & 2_{+4} \\ 2_{-2} & 0_{+4} & -1_{-8} \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1 & -2 & 4 \\ 0 & -1 & 6 \\ 0 & 4_{-4} & -9_{+24} \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1 & -2 & 4 \\ 0 & -1 & 6 \\ 0 & 0 & 15 \end{array} \right) 
\end{align*} 
\]と変形できるので、行列 \( A \) の階数は3*2。

ベクトルの本数は3本に対し、行列 \( A \) の階数も3なので、1次独立である。

 

パターン2　行列式で判別する方法

行列 \( A \) の行列式は、\[
\begin{align*}  |A| = &
\left| \begin{array}{ccc} 1 & -2 & 4 \\ -1 & 1 & 2 \\ 2 & 0 & -1 \end{array} \right|
\\ = & -1 - 8 + 0 - (8 - 2 - 0)
\\ = & -9 - 6
\\ = & -15 \not = 0
\end{align*}  \]となるので行列 \( A \) は正則。

よって１次独立である。

 

 

(2)  \[
\vec{a_1} = \left( \begin{array}{ccc} 1 \\ 2 \\ 3   \end{array} \right) \ \ \ 
\vec{a_2} = \left( \begin{array}{ccc} -1 \\ 1 \\ 3   \end{array} \right) \ \ \ 
\vec{a_3} = \left( \begin{array}{ccc} 6 \\ 3 \\ 0   \end{array} \right) \ \ \ 
\vec{a_4} = \left( \begin{array}{ccc} 1 \\ 0 \\ -1   \end{array} \right) \ \ \ 
\]

行列 \( A \) を\[ A = \left( \vec{a_1}, \vec{a_2}, \vec{a_3}, \vec{a_4} \right) = 
\left( \begin{array}{ccc} 1 & -1 & 6 & 1 \\ 2 & 1 & 3 & 0 \\ 3 & 3 & 0 & -1 \end{array} \right) \]とする。\[
\begin{align*} &
\left( \begin{array}{ccc} 1 & -1 & 6 & 1 \\ 2_{-2} & 1_{+2} & 3_{-12} & 0_{-2} \\ 3_{-3} & 3_{+3} & 0_{-18} & -1_{-3} \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1_{\times 2} & -1_{\times 2} & 6_{\times 2} & 1_{\times 2} \\ 0 & 3 & -9 & -2 \\ 0 & 6_{-6} & -18_{+18} & -4_{+4} \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 2 & -2_{+3} & 12_{-9} & 2_{-2} \\ 0 & 3 & -9 & -2 \\ 0 & 0 & 0 & 0 \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 2 & 1 & 3 & 0 \\ 0 & 3 & -9 & -2 \\ 0 & 0 & 0 & 0 \end{array} \right)
\end{align*}
\]と変形できるので、行列 \( A \) の階数は2。ベクトルの本数は4なので1次従属である。

1次関係式は行基本変形後の行列からできるベクトルを \( \vec{b_1} \), \( \vec{b_2} \), \( \vec{b_3} \), \( \vec{b_4} \) とすると、\[
\vec{b_1} = \left( \begin{array}{ccc} 2 \\ 0 \\ 0   \end{array} \right) \ \ \ 
\vec{b_2} = \left( \begin{array}{ccc} 1 \\ 3 \\ 0   \end{array} \right) \ \ \ 
\vec{b_3} = \left( \begin{array}{ccc} 3 \\ -9 \\ 0   \end{array} \right) \ \ \ 
\vec{b_4} = \left( \begin{array}{ccc} 0 \\ -2 \\ 0   \end{array} \right) \ \ \ 
\]である。よって関係式として例えば\[
\vec{b_1} - 3\vec{b_4} = 2 \vec{b_2} \\
3 \vec{b_1} + 9 \vec{b_4} = 2\vec{b_3}
\]が挙げられる（どちらでもOK）。

 

解答2

行列 \( A \) を\[ A = \left( \vec{a_1}, \vec{a_2}, \vec{a_3}\right) = 
\left( \begin{array}{ccc} 1 & 1 & 2 \\ 0 & 1 & 1 \\ 1 & x & -1 \end{array} \right) \]とします。

 

パターン1　行列式を使う方法

1次従属になるためには行列 \( A \) の行列式が0になればよい*3。\[
\begin{align*}  |A| = &
\left| \begin{array}{ccc} 1 & 1 & 2 \\ 0 & 1 & 1 \\ 1 & x & -1 \end{array} \right|
\\ = & -1 + 1 - (2 + x)
\\ = & -2 - x = 0
\end{align*}  \]となればいいので、\( x = -2 \) のとき1次従属となる。

 

パターン2　行基本変形で階数を求める

1次従属になるためには、\[
\mathrm{rank} \ A < n = 3
\]が成り立てばよい。

\[
\begin{align*} &
\left( \begin{array}{ccc} 1 & 1 & 2 \\ 0 & 1 & 1 \\ 1_{-1} & x_{-1} & -1_{-2} \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1 & 1 & 2 \\ 0 & 1 & 1 \\ 0 & x-1_{+3} & -3_{+3} \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1 & 1 & 2 \\ 0 & 1 & 1 \\ 0 & x+2 & 0 \end{array} \right)
\end{align*} 
\]と変形できる。

よって、\( x = -2 \) のとき階数が2 < 3となるので1次従属となる。

 

解答3

行列 \( A \) を\[ A = \left( \vec{a_1}, \vec{a_2}, \vec{a_3}\right) = 
\left( \begin{array}{ccc} 0 & 1 & -1 & 0 & 2 \\ 3 & 0 & 1 & 7 & 3 \\ 1 & -2 & -4 & -4 & -3 \\ 1 & -1 & -2 & -1 & -1 \end{array} \right) \]とする。\[
\begin{align*} &
\left( \begin{array}{ccc} 0 & 1 & -1 & 0 & 2 \\ 3_{-3} & 0_{+3} & 1_{+6} & 7_{+3} & 3_{+3} \\ 1_{-1} & -2_{+1} & -4_{+2} & -4_{+1} & -3_{+1} \\ 1 & -1 & -2 & -1 & -1 \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 0 & 1 & -1 & 0 & 2 \\ 0 & 3_{-3} & 7_{+3} & 10 & 6_{-6} \\ 0 & -1_{+1} & -2_{-1} & -3 & -2_{+2} \\ 1 & -1_{+1} & -2_{-1} & -1 & -1_{+2} \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 0 & 1 & -1 & 0 & 2 \\ 0 & 0 & 10_{-10} & 10_{-10} & 0 \\ 0 & 0 & -3_{\div (-3)} & -3_{\div (-3)} & 0 \\ 1 & 0 & -3 & -1 & 1 \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1 & 0 & -3_{+3} & -1_{+3} & 1 \\ 0 & 1 &  -1_{+1} & 0_{+1} & 2 \\ 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1 & 0 & 0 & 2 & 1 \\ 0 & 1 &  0 & 1 & 2 \\ 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array} \right) 
\end{align*}
\]と変形できる。

行列 \( A \) の階数は3なので、1次独立なベクトルの最大数は3となる。

また、最大組は \( \vec{a_1} \), \( \vec{a_2} \), \( \vec{a_3} \) である。

ここで行基本変形後の行列 \( B \) からなるベクトルを\[
B = \left( \vec{b_1}, \vec{b_2}, \vec{b_3}, \vec{b_4} , \vec{b_5} \right)
\]とすると、\[
\vec{b_1} = \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \\ 0   \end{array} \right) \ \ \ 
\vec{b_2} = \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \\ 0   \end{array} \right) \ \ \ 
\vec{b_3} = \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \\ 0   \end{array} \right) \ \ \ 
\vec{b_4} = \left( \begin{array}{ccc} 2 \\ 1 \\ 1 \\ 0   \end{array} \right) \ \ \
\vec{b_5} = \left( \begin{array}{ccc} 1 \\ 2 \\ 0 \\ 0   \end{array} \right) 
\] となります。

ここで、\[ \vec{b_4} = 2 \vec{b_1} + \vec{b_2} + \vec{b_3} \\ \vec{b_5} = \vec{b_1} + 2 \vec{b_2} \]という関係式が成り立つので、\( \vec{a_4} \), \( \vec{a_5} \) を \( \vec{a_1} \), \( \vec{a_2} \), \( \vec{a_3} \) の1次結合で表すと、\[ \vec{a_4} = 2 \vec{a_1} + \vec{a_2} + \vec{a_3} \\ \vec{a_5} = \vec{a_1} + 2 \vec{a_2} \]となる。

 

1次結合で表す必要がない場合には、行基本変形後の列ごとの下に続く0の数に注目し、場合分けを行うことで最大組を出すのが早いです。

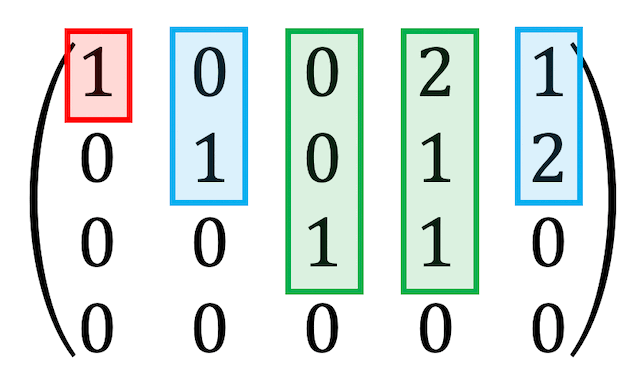
今回の場合は、このように場合分けができるので、最大組は \( \vec{a_1} \), \( \vec{a_2} \), \( \vec{a_3} \) であることがわかります。
（グループごとに異なるベクトルを選んでいればOKなので、最大組を \( \vec{a_1} \), \( \vec{a_3} \), \( \vec{a_5} \) などとするのもOK）

 

６．さいごに

今回はベクトルの1次独立、1次従属についての説明をしました。

1次独立、1次従属はこれから学ぶ線形代数でも出てきますので確実に覚えておくようにしましょう。

次回は基底についてのまとめを書きたいと思います。