うさぎでもわかる線形代数　第11羽　線形写像（前編）　線形写像の判定・表現行列

こんにちは、ももやまです。

今回は線形代数の重要な概念の1つである線形写像（線形変換）について3回にわけてまとめていきたいと思います。

前回の線形代数の記事はこちら！
グラムシュミットの直交化法についてです。

www.momoyama-usagi.com

スポンサードリンク

１．写像とは

例えば\( y = 2x + 3 \) という関数とします。
この関数に \( x = 0 \) を入れると \( y \) は3に、\( x = 1 \) を入れると \( y \) は5になりますね。

このように、何かしらの値 \( x \) を入れるととある規則に沿って何かしらの値 \( y \) を返すものを関数と呼びます。

関数の上位互換バージョンに写像があります。
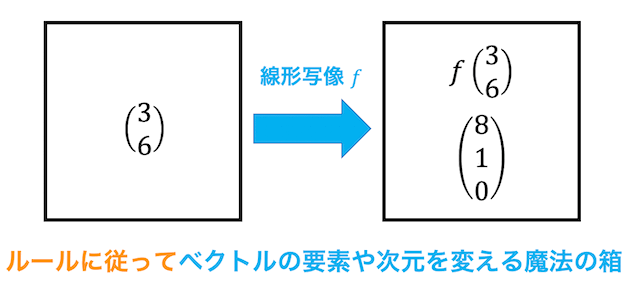
写像は、集合 \( X \) の各要素に対して、集合 \( Y \) の要素がただ1つ対応している関係を表します。言い換えると、写像は集合 \( X \) の要素を入れると集合 \( Y \) の要素を1つ返す魔法の箱といえますね。

写像について（線形写像ではない）のもっと詳しい説明を見たい人は、こちらの記事をご覧ください。

www.momoyama-usagi.com

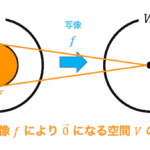
線形写像は写像のベクトルバージョンで、ルールに従ってベクトルの要素や次元を変える魔法の箱です。

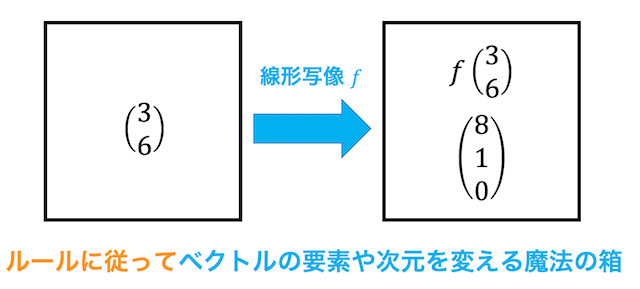
しかし、線形写像には、ベクトル空間からベクトル空間において、つぎの条件を満たしていなければなりません。

また、同じベクトル空間同士（ベクトル空間 \( V \) から \( V \) ）への変換を特に線形変換と呼びます。

では、線形写像かどうかの判定を例題でやってみましょう。

例題1

次の(1)〜(7)の \( \mathbb{R}^2 \) から \( \mathbb{R}^2 \) への写像は線形写像かどうかを判定しなさい。

(1) \[ f \left( \begin{array}{ccc} x \\ y \end{array} \right)  = \left( \begin{array}{ccc} 2x-3y \\  -x+2y \end{array} \right) \]

(2) \[ f \left( \begin{array}{ccc} x \\ y \end{array} \right)  = \left( \begin{array}{ccc} x^2 \\  x+y \end{array} \right) \]

(3) \[ f \left( \begin{array}{ccc} x \\ y \end{array} \right)  = \left( \begin{array}{ccc} 0 \\ 0 \end{array} \right) \]

(4) \[ f \left( \begin{array}{ccc} x \\ y \end{array} \right)  = \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right) \]

解説1

(1)

行列を用いて表すと、\[
\left( \begin{array}{ccc} 2 & -3 \\  -1 & 2 \end{array} \right) \left( \begin{array}{ccc} x \\ y \end{array} \right) = \left( \begin{array}{ccc} 2x-3y \\  -x+2y \end{array} \right)
\]となる。ここで、\[
f( \vec{x} + \vec{y}) = A( \vec{x} + \vec{y}) = A \vec{x} + A \vec{y} \]\[
f\vec{x} + f\vec{y} = A \vec{x} + A \vec{y}
\]となるので、\[
f( \vec{x} + \vec{y}) = f\vec{x} + f\vec{y}
\]が成立する。

また、\[
f(k \vec{x}) = A(k \vec{x}) = kA \vec{x} \]\[
k f(\vec{x}) = kA \vec{x}
\]となるので\[
f(k \vec{x}) = k f(\vec{x})
\]も成立する。

よって、線形写像である。
（線形写像であるものはこのように行列を用いて示すことができます。）

(2)

\[ \vec{x} = \left( \begin{array}{ccc} 1 \\  0 \end{array} \right) \]とする。

\[ f(2 \vec{x}) = f \left( \begin{array}{ccc} 2 \\  0 \end{array} \right) = \left( \begin{array}{ccc} 4\\  2 \end{array} \right) \]\[ 2 f ( \vec{x} ) = 2 f \left( \begin{array}{ccc} 1 \\  0 \end{array} \right) = \left( \begin{array}{ccc} 2 \\  2 \end{array} \right) \]となり、\[
f(k \vec{x}) = k f(\vec{x})
\]を満たさない例があるため、線形写像ではない。

(3)

行列を用いて表すと、\[
\left( \begin{array}{ccc} 0 & 0 \\  0 & 0 \end{array} \right) \left( \begin{array}{ccc} x \\ y \end{array} \right) = \left( \begin{array}{ccc} 0 \\  0 \end{array} \right)
\]となる。

あとは(1)と同じように示せるため、線形写像。

(4)

\[ \vec{x} = \left( \begin{array}{ccc} 1 \\  0 \end{array} \right) \]とする。

\[ f(2 \vec{x}) = f \left( \begin{array}{ccc} 2 \\  0 \end{array} \right) = \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right) \]\[ 2 f ( \vec{x} ) = 2 f \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right) = \left( \begin{array}{ccc} 2 \\  2 \end{array} \right) \]となり、\[
f(k \vec{x}) = k f(\vec{x})
\]を満たさない例があるため、線形写像ではない。

スポンサードリンク

２．表現行列

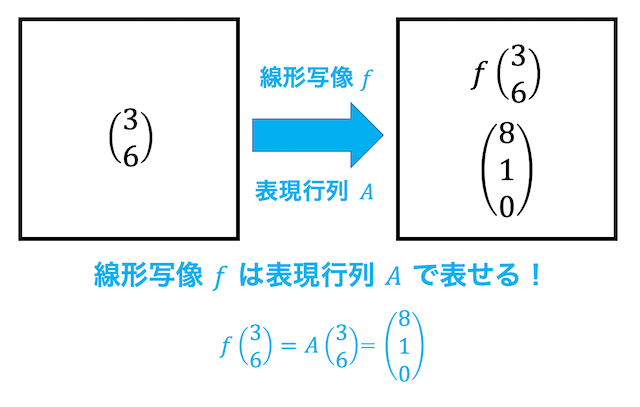
線形写像は入れたベクトルによって別のベクトルが出てくる魔法の箱と先ほど説明しましたね。

先ほど線形写像の条件を2つ説明しました。この2つの条件により、魔法の箱でかかる魔法（つまり写像）を行列を用いて表すことができるようになります。

線形写像 \( f \) は行列 \( A \) を用いて、\[
f(\vec{x} ) = A \vec{x}
\]と表すことができます。

この行列 \( A \) のことを表現行列と呼びます。

表現行列を用いることで、線形写像を行列のように扱うことができるようになります。

しかし、表現行列は変換元の空間の基底と変換先の空間の基底によって変わってきます。

なので、変換元、変換先がともに標準基底であるかそうでないかの2パターンにわけて表現行列の求め方を説明していきたいと思います。

※問題文で特に基底の指示が書かれていない場合、変換元も変換先も標準基底同士で写像を適用するものだと思ってください。

(1) 互いに標準基底同士の場合

例えば2次元空間から3次元空間（\( \mathbb{R}^2 \to \mathbb{R}^3 \)）の線形写像 \( f \) について考えてみましょう。

例えば \[
f \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right) = \left( \begin{array}{ccc} 2 \\ -1 \\ 3 \end{array} \right)  \]\[
f \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right) = \left( \begin{array}{ccc} 1 \\ 2 \\ -1 \end{array} \right)
\]という線形写像 \( f \) があるとします。

このとき、それぞれのベクトルは2次元標準基底\[
\vec{e_1} = \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right) \ \ \
\vec{e_2} = \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right)
\]および3次元標準基底\[
\vec{g_1} = \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right) \ \ \
\vec{g_2} = \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \end{array} \right) \ \ \
\vec{g_3} = \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \end{array} \right)
\]を用いて、\[
f \left( \vec{e_1} \right) = 2 \vec{g_1} - \vec{g_2} + 3 \vec{g_3} \]\[
f \left( \vec{e_2} \right) = \vec{g_1} + 2\vec{g_2} - \vec{g_3}
\]と表せます。これを行列を用いて書くと、\[\begin{align*}
\left( \ f \left( \vec{e_1} \right), f \left( \vec{e_2} \right) \right) & = \left( \vec{g_1}, \vec{g_2}, \vec{g_3} \right) \left( \begin{array}{ccc} 2 & 1 \\ -1 & 2 \\ 3 & -1 \end{array} \right)
\\ & =  \left( \begin{array}{ccc} 2 & 1 \\ -1 & 2 \\ 3 & -1 \end{array} \right)
\end{align*} \]と表すことができますね。

上の式の右辺にある行列（今回は3行2列行列）が表現行列となります。

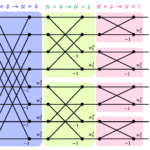
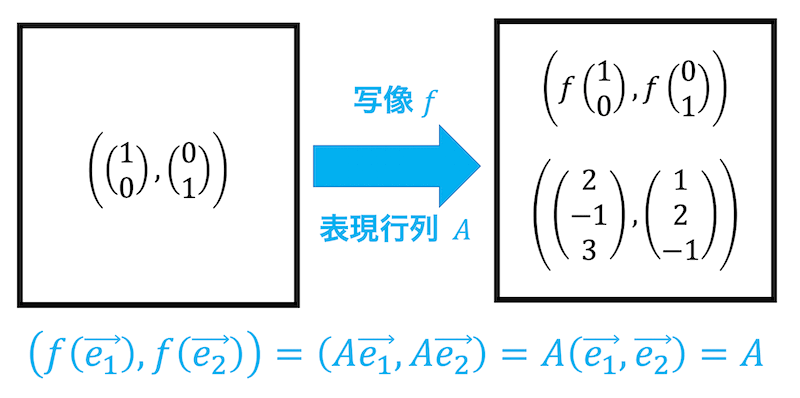
つまり、変換元も変換先も標準基底同士の場合は標準基底が移る先がそのまま表現行列になることがわかりますね。

標準基底同士の場合の表現行列 \( A \) の求め方を図示すると、以下のようになります。

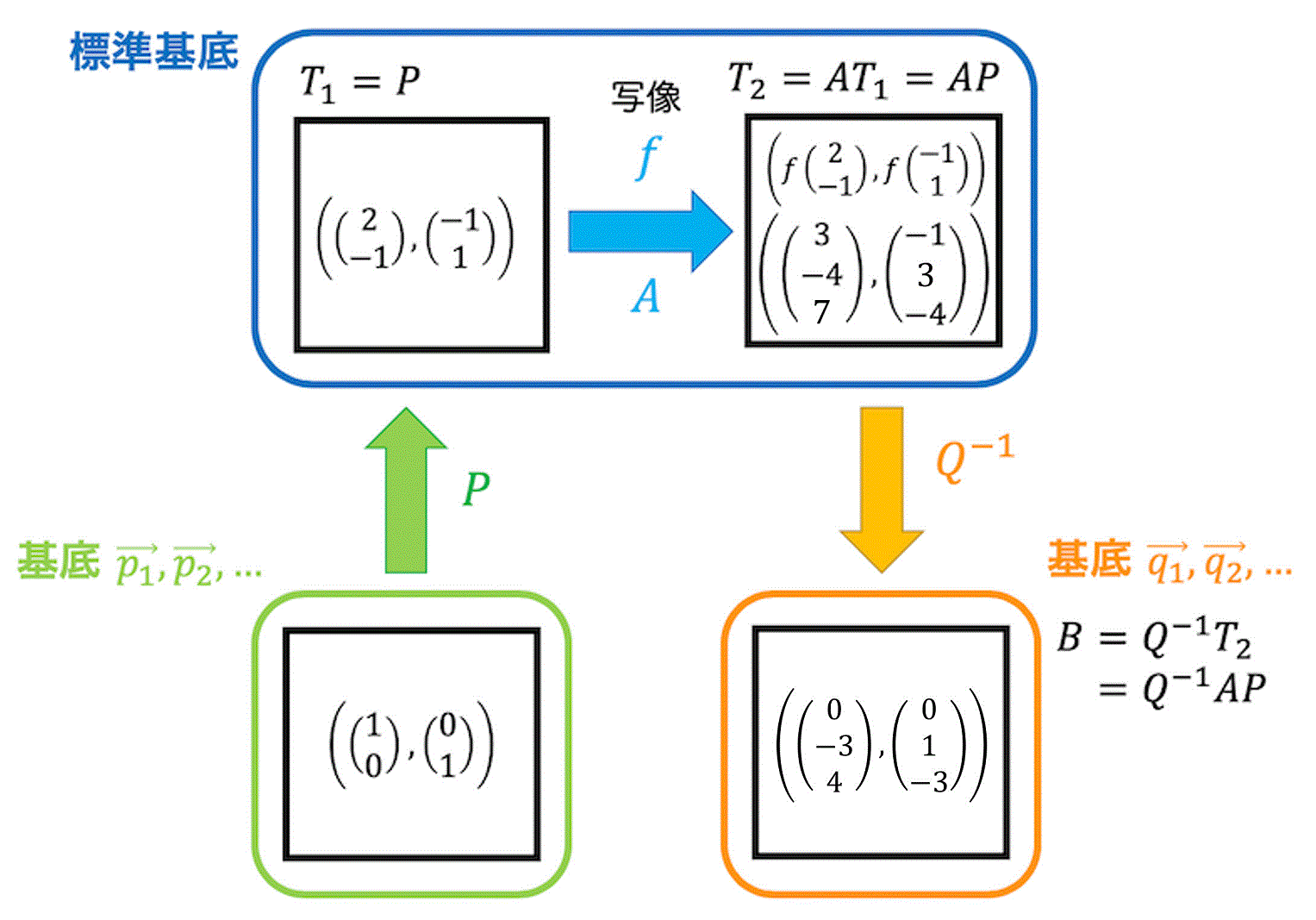
(2) 標準基底同士に限定しない場合

では標準基底同士という前提を取っ払いましょう。
標準基底ではない場合、一旦標準基底に直してから写像を適応させ、元の基底に戻する必要があるため、計算がややこしくなります。

先程と同じく2次元空間から3次元空間（\( \mathbb{R}^2 \to \mathbb{R}^3 \)）の線形写像 \( f \) について考えます。

先程と同じ \[
f \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right) = \left( \begin{array}{ccc} 2 \\ -1 \\ 3 \end{array} \right)  \]\[
f \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right) = \left( \begin{array}{ccc} 1 \\ 2 \\ -1 \end{array} \right)
\]という線形写像 \( f \) があるとします。

このとき、それぞれのベクトルの2次元の基底が、\[
\vec{p_1} = \left( \begin{array}{ccc} 2 \\ -1 \end{array} \right) \ \ \
\vec{p_2} = \left( \begin{array}{ccc} -1 \\ 1 \end{array} \right)
\]および3次元の基底が、\[
\vec{q_1} = \left( \begin{array}{ccc} 1 \\ -2 \\ 2 \end{array} \right) \ \ \
\vec{q_2} = \left( \begin{array}{ccc} -1 \\ 0 \\ -1 \end{array} \right) \ \ \
\vec{q_3} = \left( \begin{array}{ccc} 0 \\ -1 \\ 1 \end{array} \right)
\]のときの表現行列の求め方を考えてみましょう。

まずは、\[ \begin{align*}
f (\vec{p_1}) & = 2 \ f \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right) - f \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right)
\\ & = 2 \left( \begin{array}{ccc} 2 \\ -1 \\ 3 \end{array} \right) - \left( \begin{array}{ccc} 1 \\ 2 \\ -1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 3 \\ -4 \\ 7 \end{array} \right)
\end{align*} \] \[ \begin{align*}
f (\vec{p_2}) & = - f \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right) + f \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right)
\\ & = - \left( \begin{array}{ccc} 2 \\ -1 \\ 3 \end{array} \right) + \left( \begin{array}{ccc} 1 \\ 2 \\ -1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} -1 \\ 3 \\ -4 \end{array} \right)
\end{align*} \]となります。

しかし、\( f( \vec{p_1}) \), \( f( \vec{p_2}) \) の値は標準基底の値なので、基底の変換を行う必要があります。

標準基底から基底 \( \vec{q_1} \), \( \vec{q_2} \), …, \( \vec{q_m} \) に変換するためには、\[
\left( \vec{q_1}, \vec{q_2}, \cdots , \vec{q_m} \right)^{-1}  \left( f(\vec{p_1}), f(\vec{p_2}), \cdots , f(\vec{p_n}) \right)
\]と計算する必要があります。

ベクトル空間が標準基底でない場合の表現行列 \( B \) の求め方を図示すると、以下のようになります。

このように標準基底ではない場合、一旦標準基底に直してから写像 \( f \) を適用させる必要があります。
（行列の計算順序に気をつけてください。右側から順に適応していきます（\( P \), \( A \), \( Q^{-1} \) なので、\[ B = Q^{-1} AP \] と）

では例題を3つほど解いてみましょう。

例題2

\( \mathbb{R}^3 \) から \( \mathbb{R}^2 \) への線形写像 \( f \) が\[
f \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right) = \left( \begin{array}{ccc} 2 \\ 1 \end{array} \right) \ \ \
f \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \end{array} \right) = \left( \begin{array}{ccc} -1 \\ 3 \end{array} \right) \ \ \
f \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \end{array} \right) = \left( \begin{array}{ccc} 1 \\ -2 \end{array} \right)
\]を満たすとする。(1)〜(3)の問いに答えなさい。

(1) \( f \) の表現行列を求めなさい。
(2) \[ f \left( \begin{array}{ccc} 3 \\ 3 \\ 4 \end{array} \right) \]を求めなさい。
(3) \[ f \left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) \]を求めなさい。

解説2

(1)

\( \vec{e_1} \), \( \vec{e_2} \), \( \vec{e_3} \) をそれぞれ\[
\vec{e_1} = \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right) \ \ \
\vec{e_2} = \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \end{array} \right) \ \ \
\vec{e_3} = \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \end{array} \right)
\]とする。表現行列は

\[ A = \left( f( \vec{e_1}), f( \vec{e_2} ), f( \vec{e_3} ) \right) = \left( \begin{array}{ccc} 2 & -1 & 1 \\ 1 & 3 & -2 \end{array} \right) \]となる。

(2)

(1)で求めた表現行列を使う。

\[ \begin{align*}
f \left( \begin{array}{ccc} 3 \\ 3 \\ 4 \end{array} \right) = &
\ A \left( \begin{array}{ccc} 3 \\ 3 \\ 4 \end{array} \right)
\\ = & \left( \begin{array}{ccc} 2 & -1 & 1 \\ 1 & 3 & -2 \end{array} \right) \left( \begin{array}{ccc} 3 \\ 3 \\ 4 \end{array} \right)
\\ = & \left( \begin{array}{ccc} 7 \\ 4 \end{array} \right)
\end{align*} \] [別解]

\[ \begin{align*}
f \left( \begin{array}{ccc} 3 \\ 3 \\ 4 \end{array} \right) = &
\ f \left( 3 \vec{e_1} + 3 \vec{e_2} + 4 \vec{e_3} \right)
\\ = & \ 3 f ( \vec{e_1} ) + 3 f ( \vec{e_2} ) +  4 f ( \vec{e_3} )
\\ = & \ 3 \left( \begin{array}{ccc} 2 \\ 1 \end{array} \right) + 3 \left( \begin{array}{ccc} -1 \\ \ 3 \end{array} \right) + 4 \left( \begin{array}{ccc} 1 \\ -2 \end{array} \right)
\\ = & \left( \begin{array}{ccc} 7 \\ 4 \end{array} \right)
\end{align*} \]

(3)

(1)で求めた表現行列を使う。\[ \begin{align*}
f \left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = &
\ A \left( \begin{array}{ccc} x \\ y \\ z \end{array} \right)
\\ = & \left( \begin{array}{ccc} 2 & -1 & 1 \\ 1 & 3 & -2 \end{array} \right) \left( \begin{array}{ccc} x \\ y \\ z \end{array} \right)
\\ = & \left( \begin{array}{ccc} 2x-y+z \\ x+3y-2z \end{array} \right)
\end{align*} \]となる。

[別解]

\[ \begin{align*}
f \left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = &
\ f \left( x \vec{e_1} + y \vec{e_2} + z \vec{e_3} \right)
\\ = & \ x f ( \vec{e_1} ) + y f  ( \vec{e_2} ) +  z f ( \vec{e_3} )
\\ = & \ x \left( \begin{array}{ccc} 2 \\ 1 \end{array} \right) + y \left( \begin{array}{ccc} -1 \\ \ 3 \end{array} \right) + z \left( \begin{array}{ccc} 1 \\ -2 \end{array} \right)
\\ = & \left( \begin{array}{ccc} 2x - y + z \\ x + 3y - 2z \end{array} \right)
\end{align*} \]

スポンサードリンク

３．練習問題

では、練習してみましょう！

練習1

\( \mathbb{R}^2 \) から \( \mathbb{R}^3 \) への線形写像 \( f \) が\[
f \left( \begin{array}{ccc} 1 \\ 2 \end{array} \right) = \left( \begin{array}{ccc} 1 \\ 2 \\ -3  \end{array} \right) \ \ \
f \left( \begin{array}{ccc} 2 \\ 1 \end{array} \right) = \left( \begin{array}{ccc} 5 \\ 1 \\ -3 \end{array} \right)
\]を満たすとする。(1),(2)の問いに答えなさい。

(1) \[ f \left( \begin{array}{ccc} 3 \\ 3 \end{array} \right) \]の値を求めなさい。
(2) \( f \) の表現行列を求めなさい。

練習2

つぎの \( \mathbb{R}^2 \) から \( \mathbb{R}^2 \) への線形変換 \( f \) がある。\[
f \left( \begin{array}{ccc} x \\ y \end{array} \right) = \left( \begin{array}{ccc} 5x+y \\ 2x+4y \end{array} \right)
\](1)〜(3)の問いに答えなさい。

(1) 標準基底に関する \( f \) の表現行列 \( A \) を求めなさい。
(2) 基底 \( \vec{p_1} \), \( \vec{p_2} \) から基底 \( \vec{q_1} \), \( \vec{q_2} \) の線形変換 \( f \) の表現行列 \( B \) を求めなさい。\[
\vec{p_1} = \left( \begin{array}{ccc} 4 \\ 1 \end{array} \right) \ \ \ \vec{p_2} = \left( \begin{array}{ccc} 5 \\ 2 \end{array} \right) \ \ \ \vec{q_1} = \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right) \ \ \ \vec{q_2} = \left( \begin{array}{ccc} 2 \\ 1 \end{array} \right)
\] (3) 基底 \( \vec{p_1} \), \( \vec{p_2} \) 同士の線形変換 \( f \) の表現行列 \( C \) を求めなさい。\[
\vec{p_1} = \left( \begin{array}{ccc} 1 \\ -2 \end{array} \right) \ \ \ \vec{p_2} = \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right) \]

４．練習問題の答え

解答1

(1) \[ \begin{align*}
f \left( \begin{array}{ccc} 3 \\ 3 \end{array} \right)
= & f \left( \begin{array}{ccc} 1 \\ 2 \end{array} \right) + f \left( \begin{array}{ccc} 2 \\ 1 \end{array} \right) \\ = & \left( \begin{array}{ccc} 1 \\ 2 \\ -3  \end{array} \right) + \left( \begin{array}{ccc} 5 \\ 1 \\ -3 \end{array} \right)
\\ = & \left( \begin{array}{ccc} 6 \\ 3 \\ -6 \end{array} \right)
\end{align*} \]

(2) \[\begin{align*}
f \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
& = \frac{1}{3} \ f \left( \begin{array}{ccc} 3 \\ 3 \end{array} \right)
\\ & = \frac{1}{3} \left( \begin{array}{ccc} 6 \\ 3 \\ -6 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 2 \\ 1 \\ -2 \end{array} \right)
\end{align*} \]なので、\[
\begin{align*}
f \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right) & =
f \left( \begin{array}{ccc} 2 \\ 1 \end{array} \right) - f \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 5 \\ 1 \\ -3 \end{array} \right) - \left( \begin{array}{ccc} 2 \\ 1 \\ -2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 3 \\ 0 \\ -1 \end{array} \right)
\end{align*}
\]\[
\begin{align*}
f \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right) & =
f \left( \begin{array}{ccc} 1 \\ 2 \end{array} \right) - f \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 \\ 2 \\ -3 \end{array} \right) - \left( \begin{array}{ccc} 2 \\ 1 \\ -2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} -1 \\ 1 \\ -1 \end{array} \right)
\end{align*}
\]となる。よって表現行列は、\[
\left( f \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right), f \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right)  \right) = \left( \begin{array}{ccc} 3 & -1 \\ 0 & 1 \\ -1 & -1 \end{array} \right)
\]と求められる。

[別解]

\[ \begin{align*}
\left( f \left( \begin{array}{ccc} 1 \\ 2 \end{array} \right), f \left( \begin{array}{ccc} 2 \\ 1 \end{array} \right)  \right)
& =  \left( f \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right), f \left( \begin{array}{ccc} 0\\ 1 \end{array} \right)  \right) \left( \begin{array}{ccc} 1 & 2 \\ 2 & 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 & 5 \\ 2 & 1 \\ -3 & -3 \end{array} \right)
\end{align*} \]と変形できるので、\[
\begin{align*}
\left( f \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right), f \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right)  \right)
& = \left( \begin{array}{ccc} 1 & 5 \\ 2 & 1 \\ -3 & -3 \end{array} \right) \left( \begin{array}{ccc} 1 & 2 \\ 2 & 1 \end{array} \right)^{-1}
\\ & = \left( \begin{array}{ccc} 1 & 5 \\ 2 & 1 \\ -3 & -3 \end{array} \right) \cdot \frac{1}{3} \left( \begin{array}{ccc} -1 & 2 \\ 2 & -1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 3 & -1 \\ 0 & 1 \\ -1 & -1 \end{array} \right)
\end{align*}
\]と変形して表現行列を出すのもOK。

解答2

(1) \[
f \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right) = \left( \begin{array}{ccc} 5 \\ 2 \end{array} \right) \ \ \ f \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right) = \left( \begin{array}{ccc} 1 \\ 4 \end{array} \right)
\]なので、表現行列は、\[
\left( f \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right), f \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right)  \right) = \left( \begin{array}{ccc} 5 & 1 \\ 2 & 4 \end{array} \right)
\]となる。

[別解]

定義式の \( x \), \( y \) の係数に注目する。
すると、\[
A = \left( \begin{array}{ccc} 5 & 1 \\ 2 & 4 \end{array} \right)
\]となることがわかる。

(2) \[
f \left( \begin{array}{ccc} x \\ y \end{array} \right) = \left( \begin{array}{ccc} 5x+y \\ 2x+4y \end{array} \right)
\]に、\( (x,y) = (4,1) \) および \( (x,y) = (5,2) \) を代入することで\[
f \left( \begin{array}{ccc} 4 \\ 1 \end{array} \right) = \left( \begin{array}{ccc} 21 \\ 12 \end{array} \right) \ \ \ f \left( \begin{array}{ccc} 5 \\ 2 \end{array} \right) = \left( \begin{array}{ccc} 27 \\ 18 \end{array} \right)
\]が求められる。

表現行列は\[
\begin{align*}
\left( f \left( \begin{array}{ccc} 4 \\ 1 \end{array} \right), f \left( \begin{array}{ccc} 5 \\ 2 \end{array} \right)  \right)  & =  \left( \begin{array}{ccc} 21 & 27 \\ 12 & 18 \end{array} \right)
\\ & = \left( \vec{q_1}, \vec{q_2} \right) B
\\ & = \left( \begin{array}{ccc} 1 & 2 \\ 1 & 1 \end{array} \right) B
\end{align*}
\]となる。

よって、\( B \) は\[
\left( \begin{array}{ccc} 1 & 2 \\ 1 & 1 \end{array} \right) B = \left( \begin{array}{ccc} 21 & 27 \\ 12 & 18 \end{array} \right)
\]を解くことにより、求められるので、 \[
\begin{align*}
B = & \left( \begin{array}{ccc} 1 & 2 \\ 1 & 1 \end{array} \right)^{-1} \left( \begin{array}{ccc} 21 & 27 \\ 12 & 18 \end{array} \right)
\\ = & \left( \begin{array}{ccc} -1 & 2 \\ 1 & -1 \end{array} \right) \left( \begin{array}{ccc}21 & 27 \\ 12 & 18 \end{array} \right)
\\ = & \left( \begin{array}{ccc} 3 & 9 \\ 9 & 9 \end{array} \right)
\end{align*}
\]と計算できる^[1]両辺に\[\left( \begin{array}{ccc} 1 & 2 \\ 1 & 1 \end{array} \right)^{-1}\]を掛けることにより、左辺を \(  B \) としている。。

[別解]

基底行列をそれぞれ\[
P = \left( \vec{p_1}, \vec{p_2} \right) \ \ \
Q = \left( \vec{q_1}, \vec{q_2} \right)
\]とし、標準基底の表現行列 \( A \) を用いると基底 \( \vec{p_1} \), \( \vec{p_2} \) から基底 \( \vec{q_1} \), \( \vec{q_2} \) における表現行列 \( B \)は、\[
\begin{align*}
B & = Q^{-1} A P
\\ & = \left( \begin{array}{ccc} 1 & 2 \\ 1 & 1 \end{array} \right)^{-1}  \left( \begin{array}{ccc} 5 & 1 \\ 2 & 4 \end{array} \right) \left( \begin{array}{ccc} 4 & 5 \\ 1 & 2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 3 & 9 \\ 9 & 9 \end{array} \right)
\end{align*}
\]と計算できる。

(3) \[
f \left( \begin{array}{ccc} 1 \\ -2 \end{array} \right) = \left( \begin{array}{ccc} 3 \\ -6 \end{array} \right) \ \ \ f \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right) = \left( \begin{array}{ccc} 6 \\ 6 \end{array} \right)
\]なので、表現行列は\[
\begin{align*}
\left( f \left( \begin{array}{ccc} 1 \\ -2 \end{array} \right), f \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)  \right)  & =  \left( \begin{array}{ccc} 3 & 6 \\ -6 & 6 \end{array} \right)
\\ & = \left( \vec{p_1}, \vec{p_2} \right) B
\\ & = \left( \begin{array}{ccc} 1 & 1 \\ -2 & 1 \end{array} \right) C
\end{align*}
\]となる。

よって表現行列 \( C \) は、\[
\begin{align*}
C = & \left( \begin{array}{ccc} 1 & 1 \\ -2 & 1 \end{array} \right)^{-1} \left( \begin{array}{ccc} 3 & 6 \\ -6 & 6 \end{array} \right)
\\ = & \frac{1}{3} \left( \begin{array}{ccc} 1 & -1 \\ 2 & 1 \end{array} \right) \left( \begin{array}{ccc} 3 & 6 \\ -6 & 6 \end{array} \right)
\\ = & \left( \begin{array}{ccc} 3 & 0 \\ 0 & 6 \end{array} \right)
\end{align*}
\]と計算できる。

[別解]

基底行列をそれぞれ\[
P = \left( \vec{p_1}, \vec{p_2} \right)
\]とし、標準基底の表現行列 \( A \) を用いると基底 \( \vec{p_1} \), \( \vec{p_2} \) から基底 \( \vec{p_1} \), \( \vec{p_2} \) における表現行列 \( C \)は、\[
\begin{align*}
C & = P^{-1} A P
\\ & =\left( \begin{array}{ccc} 1 & -1 \\ 2 & 1 \end{array} \right)^{-1}  \left( \begin{array}{ccc} 5 & 1 \\ 2 & 4 \end{array} \right) \left( \begin{array}{ccc} 1 & -1 \\ 2 & 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 3 & 0 \\ 0 & 6 \end{array} \right)
\end{align*}
\]と計算できる。

（ \( P^{-1} AP \) は対角化でも出てくる重要な形です）

５．さいごに

今回は線形写像（線形変換）についてのまとめを行いました。

標準基底同士の場合は標準基底の行き先を並べたものがそのまま表現行列に、標準基底同士ではない場合は、一旦標準基底になおして、写像を適用し、再びもとに戻した結果が表現行列になることを頭に入れておきましょう。

次回は線形写像における合成写像・逆変換（逆写像）についてまとめていきたいと思います。