表現行列 \( A \) で表されるベクトル空間 \( V \)（ \( \mathbb{R}^n \) ）からベクトル空間 \( W \)（ \( \mathbb{R}^m \) ）への線形写像 \( f \) があるとします。このとき、\[
f ( \vec{x} ) = A \vec{x}
\]と表すことができますね。

例えば、\( \vec{x} = \vec{0} \) を考えて見ましょう。すると当然\[
A \vec{0} = \vec{0}
\]となりますね。

しかし、\[
A \vec{x} = \vec{0}
\]を満たすような \( \vec{x} \) は \( \vec{0} \) 以外にも存在する可能性はありますよね。

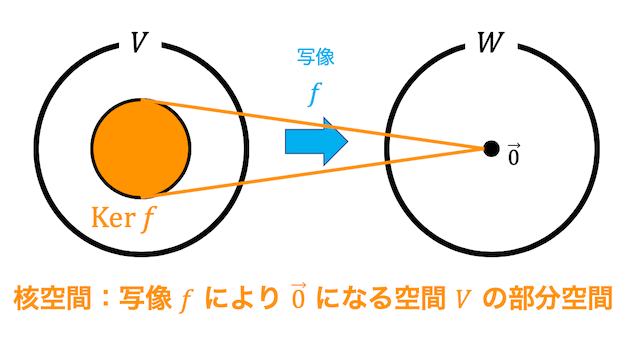
つまり、核空間は線形写像 \( f \) により \( \vec{0} \) になってしまうようなベクトル空間 \( V \) の一部（部分空間）を表します。

線形写像 \( f \) の核空間のことを \( \mathrm{Ker} \ f \) と表します。

核空間（Ker f）の定義

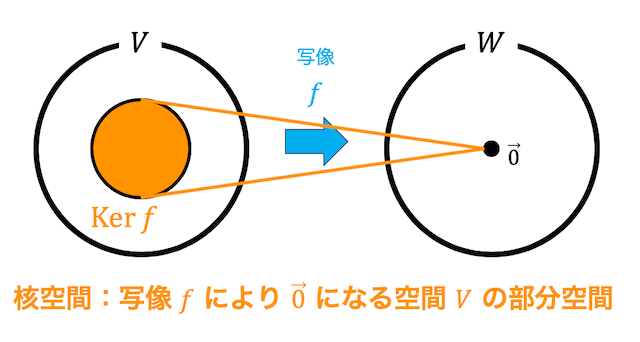
ベクトル空間\( V \) からベクトル空間 \( W \) への線形写像 \( f \) で、\[
\mathrm{Ker} \ f = \left\{ \vec{x} \in V \ \middle| \ f( \vec{x} ) = \vec{0} \right\}
\]を \( f \) の核空間（カーネル）と呼びます。

（わかりやすく言うと、連立方程式\[
f( \vec{x} ) = A \vec{x} = \vec{0}
\]の解の集合（解空間）が核空間（カーネル）となる。）

例題1

行列 \( A \) を\[
A = \left( \begin{array}{ccc} 2 & 5 & -3 \\ 3 & -3 & -1 \\ 1 & -8 & 2 \end{array} \right)
\]とする。このとき、\( \mathbb{R}^3 \) から \( \mathbb{R}^3 \) 、\( f(\vec{x}) = A \vec{x} \) と定義される線形写像 \( f \) が表す核の次元と基底を答えなさい。

解説1

\[
\mathrm{Ker} \ f = \left\{ \vec{x} \in \mathbb{R}^3 \ \middle| \ f( \vec{x} ) = \vec{0} \right\} = \left\{ \vec{x} \in\mathbb{R}^3 \ \middle| \ A \vec{x} = \vec{0} \right\}
\]なので、解空間の部分空間を求めればOK。

連立方程式を解くために行列 \( A \) を掃き出します。\[
\begin{align*} &
\left( \begin{array}{ccc} 2_{-2} & 5_{+16} & -3_{-4} \\ 3_{-3} & -3_{+24} & -1_{-6} \\ 1 & -8 & 2 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 0 & 21 & -7 \\ 0 & 21 & -7 \\ 1 & -8 & 2 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 0 & 21_{-21} & -7_{+7} \\ 0 & 21_{\div 7} & -7_{\div 7} \\ 1 & -8_{+6} & 2_{-2} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 0 & 0 & 0 \\ 0 & 3 & -1 \\ 1 & -2 & 0 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & -2 & 0 \\ 0 & 3 & -1 \\ 0 & 0 & 0 \end{array} \right)
\end{align*}
\]となるので、\[
\left\{ \begin{array}{l} x-2y= 0 \\ 3y - z = 0 \end{array}\right.
\]と同じ連立方程式となることがわかる（自由度1）。

ここで、\( y = t \) とすると \( x = 2t \), \( z = 3t \) となることがわかる。ベクトルで書くと\[ \vec{x} =
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right)
= t \left( \begin{array}{ccc} 2 \\ 1 \\ 3 \end{array} \right)
\]となる。

つまり、解ベクトル \( \vec{x} \) を表現するためには、\[\left( \begin{array}{ccc} 2 \\ 1 \\ 3 \end{array} \right) \]の1つのベクトルがあればよい。よって、\[
\mathrm{Ker} \ f = \left\{ \ \left( \begin{array}{ccc} 2 \\ 1 \\ 3 \end{array} \right) \ \right\}
\]となり、\( \dim \mathrm{Ker} \ f = 1 \) （1次元）となります。

なお、核空間の次元（ \( \dim \mathrm{Ker} \ f \) ）は、解空間の部分空間と同じように行列 \( A \) の階数を用いても判定することができます。

今回の場合だと、\[
\dim V = n - \mathrm{Rank} \ A = 3 - 2 = 1
\]と求められます（\( n \) は写像元の次元の大きさ）。

核空間（Ker f）の次元と表現行列の階数の関係

表現行列 \( A \) で表される \( \mathbb{R}^n \) から \( \mathbb{R}^m \) への線形写像 \( f \) の核の次元の大きさ \( \dim \mathrm{Ker} \ f \) は、\[
\dim \mathrm{Ker} \ f = n - \mathrm{Rank} \ A
\]で求められる*1。

核空間の次元のことを退化次数とも呼びます。

スポンサードリンク

２．像空間

先ほどと同じく表現行列 \( A \) で表されるベクトル空間 \( V \)（ \( \mathbb{R}^n \) ）からベクトル空間 \( W \)（ \( \mathbb{R}^m \) ）への線形写像 \( f \) があるとします。

このとき、\[
f ( \vec{x} ) = A \vec{x}
\]と表すことができますね（ここまでは全く同じ）。

このとき、ベクトル \( \vec{x} \) を動かすと線形写像 \( f \) を適用した \( f ( \vec{x} ) \) も動きますね。しかし、\( f ( \vec{x} ) \) が動く範囲にはもちろん限りがあります。

像空間はベクトル \( \vec{x} \) をベクトル空間 \( V \) の範囲で値を変えたときに線形写像 \( f \) を適用した \( f(\vec{x}) \) が取りうる空間の範囲を表します。

線形写像 \( f \) の像空間のことを \( \mathrm{Im} \ f \) と表します。

像空間（Im f）の定義

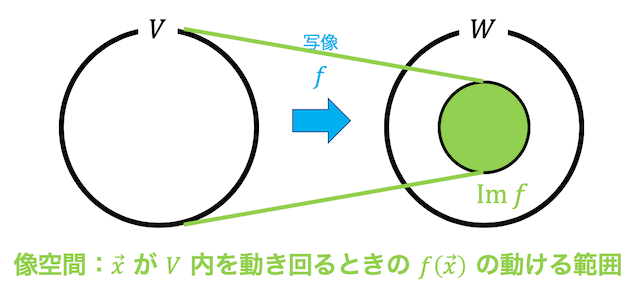
ベクトル空間\( V \) からベクトル空間 \( W \) への線形写像 \( f \) で、\[
\mathrm{Im} \ f = \left\{ f( \vec{x} ) \ \middle| \ \vec{x} \in V \right\}
\]を \( f \) の像空間（イメージ）と呼びます。

（わかりやすく言うと、\( f( \vec{x}) \) が動く範囲をベクトルの集合で表したものが像空間（イメージ）となる。）

例題2

行列 \( A \) を\[
A = \left( \begin{array}{ccc} 2 & 5 & -3 \\ 3 & -3 & -1 \\ 1 & -8 & 2 \end{array} \right)
\]とする（例題1と同じ）。

このとき、\( \mathbb{R}^3 \) から \( \mathbb{R}^3 \) 、\( f(\vec{x}) = A \vec{x} \) と定義される線形写像 \( f \) が表す像の次元と基底を答えなさい。

解説2

\[
\mathrm{Im} \ f = \left\{ f( \vec{x} ) \ \middle| \ \vec{x} \in V \right\} = \left\{ A\vec{x} \ \middle| \ \vec{x} \in V \right\}
\]となる。ここで、\[
\vec{x} =\left( \begin{array}{ccc} c_1 \\ c_2 \\ c_3 \end{array} \right)
\]とすると、\[\begin{align*}
A \vec{x} & = \left( \begin{array}{ccc} 2 & 5 & -3 \\ 3 & -3 & -1 \\ 1 & -8 & 2 \end{array} \right)\left( \begin{array}{ccc} c_1 \\ c_2 \\ c_3 \end{array} \right)
\\ & = c_1 \left( \begin{array}{ccc} 2 \\ 3 \\ 1 \end{array} \right) + c_2 \left( \begin{array}{ccc} 5 \\ -3 \\ -8 \end{array} \right) + c_3 \left( \begin{array}{ccc} -3 \\ -1 \\ 2 \end{array} \right)
\end{align*} \]となる。

よって \( f \) の像空間は\[
\left< \ \left( \begin{array}{ccc} 2 \\ 3 \\ 1 \end{array} \right) , \left( \begin{array}{ccc} 5 \\ -3 \\ -8 \end{array} \right), \left( \begin{array}{ccc} -3 \\ -1 \\ 2 \end{array} \right) \right>
\]で生成される（張られる）部分空間となる。

つまり、生成される3つのベクトル内の中から選び出せる1次独立な最大組と最大数がそのまま \( \mathrm{Im} \ f \) の基底と次元となる。\[
\begin{align*} &
\left( \begin{array}{ccc} 2_{-2} & 5_{+16} & -3_{-4} \\ 3_{-3} & -3_{+24} & -1_{-6} \\ 1 & -8 & 2 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 0 & 21 & -7 \\ 0 & 21 & -7 \\ 1 & -8 & 2 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 0 & 21_{-21} & -7_{+7} \\ 0 & 21_{\div 7} & -7_{\div 7} \\ 1 & -8_{+6} & 2_{-2} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 0 & 0 & 0 \\ 0 & 3 & -1 \\ 1 & -2 & 0 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & -2 & 0 \\ 0 & 3 & -1 \\ 0 & 0 & 0 \end{array} \right)
\end{align*}
\]となる（さっきと全く同じ変形）。

よって像の基底、つまり1次独立なベクトルの最大組は、\[
\left\{ \
\left( \begin{array}{ccc} 2 \\ 3 \\ 1 \end{array} \right) , \
\left( \begin{array}{ccc} 5 \\ -3 \\ -8 \end{array} \right) \
\right\}
\]となり、\( \dim \mathrm{Im} \ f = 2 \) （2次元）となります。

線形写像の像の基底と次元を求める際には表現行列のそれぞれの列を\[
A = \left( \vec{a_1}, \vec{a_2}, \cdots, \vec{a_n} \right)
\]のようにベクトルとし、さらに解ベクトル \( \vec{x} \) を\[
\vec{x} = \left( \begin{array}{ccc} c_1 \\ c_2 \\ \vdots \\ c_n \end{array} \right)
\]と見ることで、\[
A \vec{x} = c_1 \vec{a_1} + c_2 \vec{a_2} + \cdots c_n \vec{a_n}
\]のような1次結合となり、生成系の部分空間\[
\left< \vec{a_1}, \vec{a_2}, \cdots, \vec{a_n} \right>
\]を求める問題に変えることができます。

なので像空間の次元（ \( \dim \mathrm{Im} \ f \) ）も、核空間と同じように行列 \( A \) の階数を用いても判定することができます。

今回の場合だと、\[
\dim \mathrm{Im} \ f = \mathrm{Rank} \ A = 2
\]と求められます。

像空間（Im f）の次元と表現行列の階数の関係

表現行列 \( A \) で表される \( \mathbb{R}^n \) から \( \mathbb{R}^m \) への線形写像 \( f \) の像の次元の大きさ \( \dim \mathrm{Im} \ f \) は、\[
\dim \mathrm{Im} \ f = \mathrm{Rank} \ A
\]で求められる。

スポンサードリンク

３．次元定理

線形写像における核空間は写像によって \( \vec{0} \) につぶれてしまう空間を表し、像空間は写像を適用してもそのまま残る空間を表します。

なので、下のような定理が成立します。

次元定理

表現行列 \( A \) で表される \( \mathbb{R}^n \) から \( \mathbb{R}^m \) への線形写像 \( f \) では、\[
\dim \mathrm{Ker} \ f + \dim \mathrm{Im} \ f = n
\]が成立する。

（\( n \) は表現行列の列数に相当）

この定理は有名で、次元定理、次元公式、階数・退化次数の定理などと呼ばれます。

４．線形写像における全射・単射・全単射

核空間、像空間を調べることで線形写像が全射、単射、全単射であるかを判定することができます。

(1) 全射・単射・全単射とは

離散数学や情報数学では全射、単射について学ぶのですが、まだ未履修の方もいるかもしれないので、全射、単射とはどんなものなのかをまずは簡単に説明しましょう。

（全射、単射がわかっている人は飛ばしてもOKです！）

(a) 全射

図のような集合 \( V \) から集合 \( W \) への写像があるとしましょう。

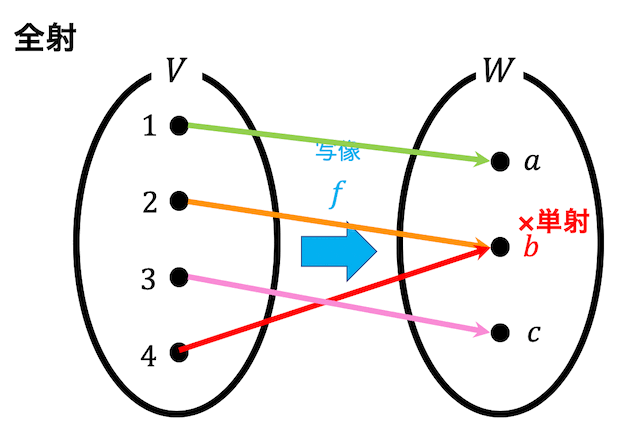
図の写像は \( W \) のどの要素も \( V \) からの対応付け（矢印）がありますよね。

このように、\( W \) の要素すべてが \( V \) のどれかの要素と対応しているような写像を全射といいます。

（この図の写像は \( W \) の要素である \( b \) に写す \( V \) の要素が2,4と2つあるため、単射ではありません。）

(b) 単射

図のような集合 \( V \) から集合 \( W \) への写像があるとしましょう。
先ほどと若干違います。

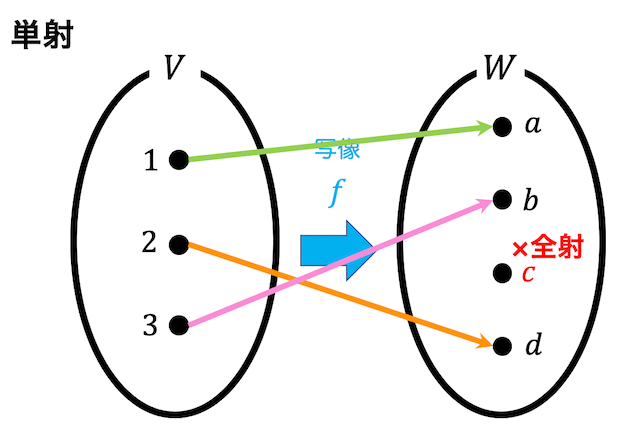
図の写像を見ると、 \( V \) の要素を変えると対応づけられている \( W \) の要素も必ず変わっていますね。

このように \( W \) のある要素に写すための \( V \) の要素は1つしかない（2つ以上存在しない）写像のことを単射といいます。

（この図の写像は \( W \) の \( c \) に写すための \( V \) の要素が存在しないため、全射ではありません。）

(c) 全単射

図のような集合 \( V \) から集合 \( W \) への写像があるとしましょう。
この図も他の2つとは若干違います。

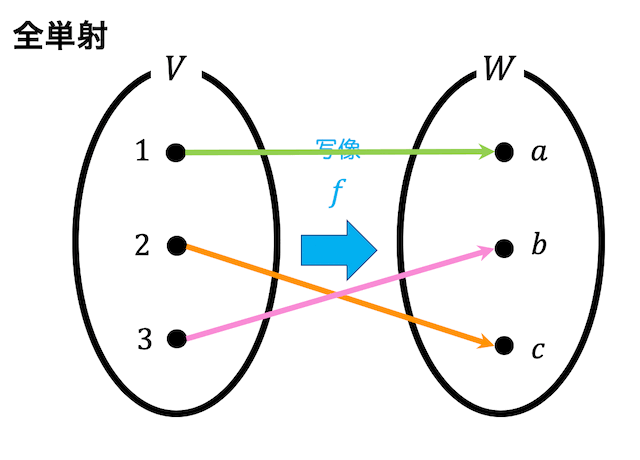
図の写像は \( W \) の要素である \( a,b,c \) すべてが \( V \) のどれかの要素と対応していますね。なので全射といえます。

また、\( W \) のそれぞれの要素に写すための \( V \) の要素は1つだけですね。なので単射といえます。

このように全射の条件・単射の条件の両方を満たすような写像を全単射と呼びます。

全単射の場合、写像は \( V \) と \( W \) に1対1の関係となります。

では、全射、単射、全単射の定義をおさらいしておきましょう。

全射・単射・全単射の定義

集合（写像元） \( V \) から集合（写像先） \( W \) への写像 \( f \) において、全射・単射・全単射というための条件は以下の通りである。

全射：写像先 \( W \) のすべての要素 \( b \) に対し、\[
f(a) = b
\] を満たすような \( V \) の要素である \( a \) が存在すること。

単射：\( V \) のすべての異なる2要素 \( a_1,a_2 \) に対して、\[
f(a_1) \not = f(a_2)
\]が成立すること。

全単射：全射の条件・単射の条件をともに満たすこと。

ゴリゴリ数式式で書いたバージョンも一応載せておきます。

全射・単射の定義（数式Ver）

数式で書くと

全射の定義\[
\forall b\in B,\,\exists a\in A \;\text{ s.t. } f(a)=b
\]

単射の定義\[
(\forall a_1, a_2 \in A)\; a_1 \neq a_2 \ \Longrightarrow \ f(a_1) \neq f(a_2)
\]

となる。

(2) 線形写像における全射、単射、全単射

全射、単射、全単射のおおまかな説明をしたところで、線形写像における全射、単射、全単射についてまとめていきましょう。

まずは、全射、単射、全単射のイメージを図で見てみましょう。

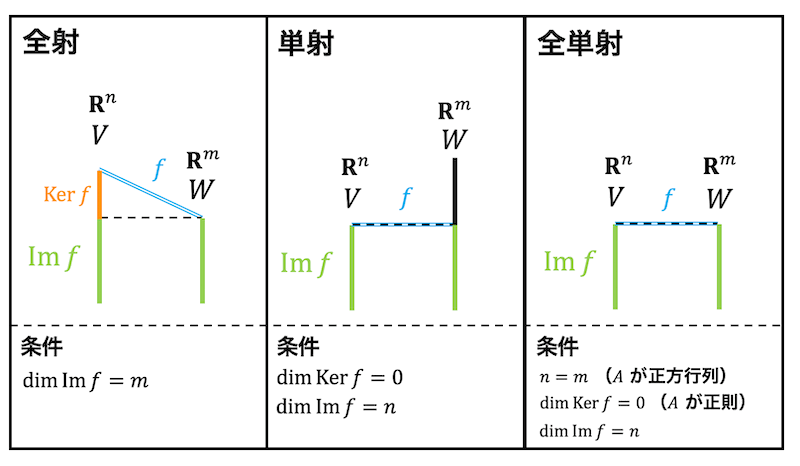
(a) 全射

全射は、\( W \) の中身すべてが \( V \) から対応付けられている状態ですね。

\( V \) の中身は核空間と像空間の2つの部分が存在するのですが、核空間は写像 \( f \) を適用するとすべて \( \vec{0} \) に飛んでしまい、潰されてしまいますね。

なので、\( W \) が全射となるためには、\( W \) の中身すべてが \( V \) の像空間から対応付けられる必要があります。

つまり、全射となるためには、\[
\dim \mathrm{Im} \ f = m = \dim W
\]となる必要がありますね。

(b) 単射

単射は、対応先 \( W \) に写す写像は2つ以上存在しないということですね。

しかし、核空間の次元が1以上だと、\( \vec{x} = \vec{0} \) のとき以外でも \( f ( \vec{x} ) = \vec{0} \) となってしまうものが存在してしまいます。

つまり、単射となるためには、\[
\dim \mathrm{Ker} \ f = 0 \Leftrightarrow \dim \mathrm{Im} \ f = n
\]となる必要がありますね。

(c) 全単射

全単射は、全射も単射も満たすものでしたね。

つまり、\[
\dim \mathrm{Im} \ f = m \\
\dim \mathrm{Ker} \ f = 0 \Leftrightarrow \dim \mathrm{Im} \ f = n \\
\]の2つをともに満たす必要があります。

条件をまとめると、\[
n = m \\
\dim \mathrm{Ker} \ f = 0 \Leftrightarrow \dim \mathrm{Im} \ f = n
\]となります。

（ちなみに \( n = m \) は表現行列 \( A \) が正方行列になる、と言い換えられます）

線形写像における全射・単射・全単射

\( m \) 行 \( n \) 列の表現行列 \( A \) で表される \( \mathbb{R}^n \) のベクトル空間 \( V \) から \( \mathbb{R}^m \) のベクトル空間 \( W \) への線形写像 \( f \) の全射・単射・全単射条件は次のようになる

線形写像 \( f \) が全射となる条件\[
\dim \mathrm{Im} \ f = m = \dim W
\]

線形写像 \( f \) が単射となる条件\[
\dim \mathrm{Ker} \ f = 0 \Leftrightarrow \dim \mathrm{Im} \ f = n
\]

線形写像 \( f \) が全単射となる（逆写像が存在する）条件\[
n = m \\
\dim \mathrm{Ker} \ f = 0 \Leftrightarrow \dim \mathrm{Im} \ f = n
\]

逆写像が存在するための条件

ここで、1つ線形写像の逆写像を思い出してみましょう。

逆写像が存在するための条件として、表現行列 \( A \) の逆行列が存在すると前説明しましたね。

表現行列 \( A \) の逆行列が存在するための条件としては、

\( A \) が正方行列
\( A \) が正則（ [tex: |A| \not = 0）

ですね。\( A \) が正方行列であるというのは、\( n = m \) であることという条件と同値ですね。また、\( A \) が正則であるというのは写像 \( f \) の核空間の次元が0であるということと同値ですね。

つまり、逆写像が存在することと、表現行列 \( A \) の逆行列が存在するということは同値であることが言えますね。

なので、表現行列 \( A \) の逆行列がうまく求めることができれば、必ず逆写像も存在するがわかりますね！

例題3

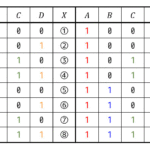
線形写像 \( f \) の表現行列が \( A \), \( B \), \( C \), \( D \) のとき、それぞれの写像 \( f \) が全射、単射であるかを判定しなさい。

(1)\[ A = \left( \begin{array}{cc} 1 & 2 \\ 3 & 1 \\ 2 & 5 \end{array} \right) \]

(2)\[ B = \left( \begin{array}{ccc} 1 & 1 & 4 \\ 3 & 3 & 4 \end{array} \right) \]

(3)\[ C = \left( \begin{array}{ccc} 1 & 2 \\ 3 & 4 \end{array} \right) \]

(4)\[ D = \left( \begin{array}{ccc} 1 & 2 \\ -2 & -4 \end{array} \right) \]

解説3

それぞれの行列の階数を出すことで、核空間の次元、像空間の次元を求めます。

(1) \[ \begin{align*}
A = & \left( \begin{array}{ccc} 1 & 2 \\ 3 & 1 \\ 2 & 5 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 2 \\ 0 & -5 \\ 0 & 1 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 2 \\ 0 & 1 \\ 0 & 0 \end{array} \right)
\end{align*} \]

より行列の階数は2→（核空間の次元は0、像空間の次元は2）。

よって\[
\dim \mathrm{Ker} \ f = 0 \\
\dim \mathrm{Im} \ f = 2 < 3 = m
\]のため、単射ではあるが全射ではない。

(2) \[ \begin{align*}
B = & \left( \begin{array}{ccc} 1 & 1 & 4 \\ 3 & 3 & 4 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 1 & 4 \\ 0 & 0 & -8 \end{array} \right)
\end{align*} \]

より行列の階数は2→（核空間の次元は1、像空間の次元は2）。

よって\[
\dim \mathrm{Ker} \ f \not = 0 \\
\dim \mathrm{Im} \ f = 2 = m
\]なので全射ではあるが単射ではない。

(3) \[ \begin{align*}
C = & \left( \begin{array}{ccc} 1 & 2 \\ 3 & 4 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 2 \\ 0 & -2 \end{array} \right)
\end{align*} \]

より行列の階数は2→（核空間の次元は0、像空間の次元は2）。

よって\[
\dim \mathrm{Ker} \ f = 0 \\
\dim \mathrm{Im} \ f = 2 = m
\]なので全射でも単射でもある（全単射）。

(4) \[ \begin{align*}
A = & \left( \begin{array}{ccc} 1 & 2 \\ -2 & -4 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 2 \\ 0 & 0 \end{array} \right)
\end{align*} \]

より行列の階数は1→（核空間の次元は1、像空間の次元は1）。

よって\[
\dim \mathrm{Ker} \ f \not = 0 \\
\dim \mathrm{Im} \ f = 1 < 2 = m
\]なので全射でも単射でもない。

５．練習問題

では、2問ほど練習をしてみましょう。

練習1

行列 \( A \) を\[
A = \left( \begin{array}{ccc} 1 & -1 & 1& 1 \\ 1 & 0 & 2 & -1 \\ 1 & 1 & 3 & -3 \end{array} \right)
\]とする。

このとき、\( \mathbb{R}^4 \) から \( \mathbb{R}^3 \) 、\( f(\vec{x}) = A \vec{x} \) と定義される線形写像 \( f \) が表す核と像の次元と基底を答えなさい。

解答1

像空間：それぞれの列をベクトルと見たときの生成系の部分空間

まずは行列 \( A \) を行基本変形します。\[
\begin{align*} &
\left( \begin{array}{ccc} 1 & -1 & 1 & 1 \\ 1_{-1} & 0_{+1} & 2_{-1} & -1_{-1} \\ 1_{-1} & 1_{+1} & 3_{-1} & -3_{-1} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & -1_{+1} & 1_{+1} & 1_{-2} \\ 0 & 1 & 1 & -2 \\ 0 & 2_{-2} & 2_{-2} & -4_{+4} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 0 & 2 & -1 \\ 0 & 1 & 1 & -2 \\ 0 & 0 & 0 & 0 \end{array} \right)
\end{align*}
\]となる。

(a) 核空間：\( A \vec{x} = \vec{0} \) の解空間

核空間の次元は \[ \dim \mathrm{Ker} \ f = n - \mathrm{Rank} \ A = 4 - 2 \]となる。

\[
\left\{ \begin{array}{l} x + 2z - w= 0 \\ y + z - 2w = 0 \end{array}\right.
\]と同じ連立方程式となることがわかる（自由度2）。

ここで、\( z = s \), \( w = t \) とすると \( x = -2s+t \), \( y = -s+2t \) となることがわかる。ベクトルで書くと\[ \vec{x} =
\left( \begin{array}{ccc} x \\ y \\ z \\ w \end{array} \right)
= s \left( \begin{array}{ccc} -2 \\ -1 \\ 1 \\ 0 \end{array} \right)
+ t \left( \begin{array}{ccc} 1 \\ 2 \\ 0 \\ 1 \end{array} \right)
\]となる。

つまり、解ベクトル \( \vec{x} \) を表現するためには、\[\left( \begin{array}{ccc} -2 \\ -1 \\ 1 \\ 0 \end{array} \right) , \left( \begin{array}{ccc} 1 \\ 2 \\ 0 \\ 1 \end{array} \right) \]の2つのベクトルがあればよい。

よって核空間の基底は、\[
\mathrm{Ker} \ f = \left\{ \ \left( \begin{array}{ccc} -2 \\ -1 \\ 1 \\ 0 \end{array} \right) , \left( \begin{array}{ccc} 1 \\ 2 \\ 0 \\ 1 \end{array} \right) \ \right\}
\]となる。

(b) 像空間：表現行列の列をベクトルと見たときの生成系の部分空間

像空間の次元は \[ \dim \mathrm{Im} \ f = \mathrm{Rank} \ A = 2 \]となる。

表現行列 \( A \) のそれぞれの列を見たとき、1次独立なベクトル2組が像空間の基底とまる。

よって像空間の基底は、\[
\mathrm{Im} \ f = \left\{ \ \left( \begin{array}{ccc} 1 \\ 1 \\ 1 \end{array} \right) , \left( \begin{array}{ccc} -1 \\ 0 \\ 1 \end{array} \right) \ \right\}
\]となる。

練習2

行列 \( A \) を\[
A = \left( \begin{array}{ccc} 1 & -1 & 0 & -2 \\ 4 & 0 & x+1 & x \\ -1 & 1 & -3 & -1 \\ 3 & 1 & -4 & -3 \end{array} \right)
\]とする。

このとき、\( \mathbb{R}^4 \) から \( \mathbb{R}^4 \) 、\( f(\vec{x}) = A \vec{x} \) と定義される線形写像 \( f \) が表す像の次元が3となるような \( x \) の値を求めなさい。また、そのときの核の次元も答えなさい。

解答2

像の次元が3ということは、行列 \( A \) の階数が3となればよい。

行列 \( A \) を行基本変形して階数を調べる。\[
\begin{align*} &
\left( \begin{array}{ccc} 1 & -1 & 0 & -2 \\ 4_{-4} & 0_{+4} & 3 & x_{+8} \\ -1_{+1} & 1_{-1} & -3 & -1_{-2} \\ 3_{-3} & 1_{+3} & -4 & -3_{+6} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & -1 & 0 & -2 \\ 0 & 4 & 3 & x+8 \\ 0 & 0 & -3 & -3 \\ 0 & 4 & -4 & 3 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & -1 & 0 & -2 \\ 0 & 4_{-4} & 3_{+4} & x+8_{-3} \\ 0 & 0 & -3 & -3 \\ 0 & 4 & -4 & 3 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & -1 & 0 & -2 \\ 0 & 0 & 7_{-7} & x+5_{-7} \\ 0 & 0 & -3 & -3 \\ 0 & 4 & -4 & 3 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & -1 & 0 & -2 \\ 0 & 0 & 0 & x-2 \\ 0 & 0 & -3 & -3 \\ 0 & 4 & -4 & 3 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & -1 & 0 & -2 \\ 0 & 4 & -4 & 3 \\ 0 & 0 & -3 & -3 \\ 0 & 0 & 0 & x-2 \end{array} \right)
\end{align*}
\]

となる。よって、\( x = 2 \) のとき、行列 \( A \) の階数は3となり、像の次元も3となる。また、\[
\dim \mathrm{Ker} \ f + \dim \mathrm{Im} \ f = n
\]が成立するので、\[
\dim \mathrm{Ker} = n - \dim \mathrm{Im} f = 4 - 3 = 1
\]となり、核の次元は1となる。
（実はこの問題は \( x \) がわからなくても核の次元は求められる）