うさぎでもわかる線形代数　第14羽　回転変換（回転行列）・対称変換

こんにちは、ももやまです。

今回は回転変換（回転行列）・対称変換についてのまとめです。

変換の中でも、原点中心に回転させる（回転変換）、原点を通るある直線 \( l \) と対称移動させる変換（対称変換）の表現行列の作り方、実際に座標を回転変換、対称変換させる方法のまとめとなっております。

前回の記事はこちら！
線形写像における核空間・像空間と線形写像における全射・単射についてです。

www.momoyama-usagi.com

スポンサードリンク

１．回転変換（2次元・平面）

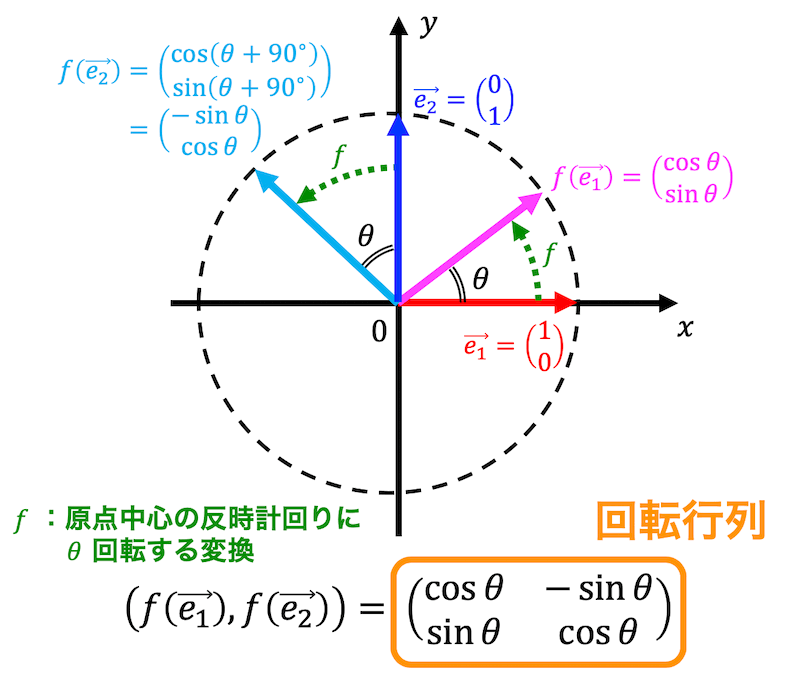
ある座標における点を原点を中心に反時計回りに \( \theta \) 回転させた点を求めるような線形変換 \( f \) の表現行列 \( A \) を考えてみましょう。

表現行列を求める際には、2次元標準基底\[
\vec{e_1} = \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right) , \ \ \
\vec{e_2} = \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right)
\]の行き先を考えればOK。

単位円を考えると、\[
x^2 + y^2 = \cos^2 \theta + \sin^2 \theta = 1
\]と変えられ、単位円上の点Aを \( ( \cos \theta, \sin \theta) \) とすることができます。
（\( \theta \) は点A (1,0) を \( 0^{\circ} \) とし、反時計回り方向を正とする）

\( \vec{e_1} \) は \( \theta = 0^{\circ} \) なので、\( \theta \) 回転させた \( f ( \vec{e_1}) \) は、\[
f( \vec{e_1} ) = \left( \begin{array}{ccc} \cos \theta \\ \sin \theta \end{array} \right)
\]となります。

同様に \( \vec{e_2} \) は \( \theta = 90^{\circ} \) なので、\( \theta \) 回転させた \( f ( \vec{e_2} ) \) は、\[ \begin{align*}
f( \vec{e_2} ) & = \left( \begin{array}{ccc} \cos (\theta + 90^{\circ}) \\ \sin (\theta +90^{\circ}) \end{array} \right)
\\ & = \left( \begin{array}{ccc} - \sin \theta  \\ \cos \theta \end{array} \right)
\end{align*} \]となります*1。

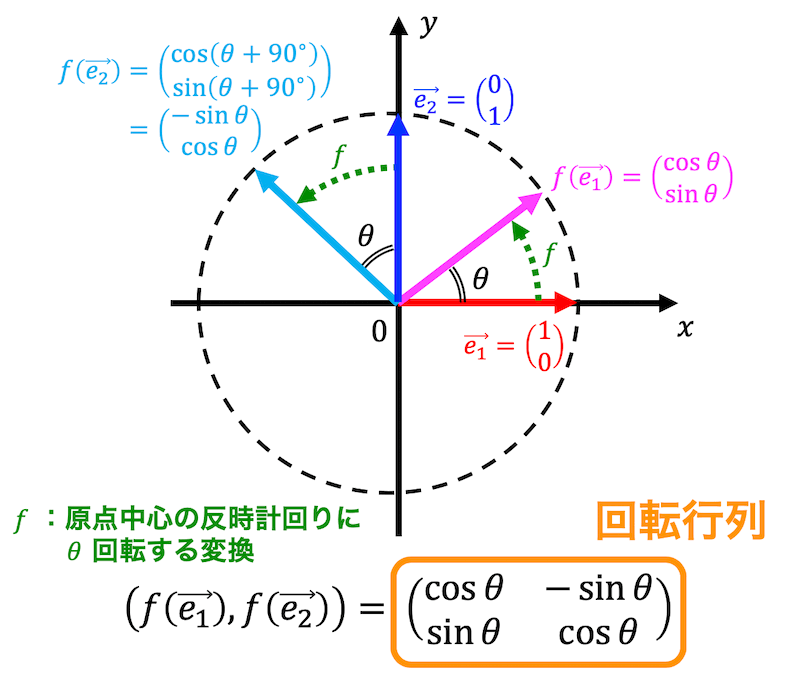
よって2次元の回転変換を表す \( f \) の表現行列 \( R( \theta ) \) は、\[
R(\theta) = \left( f ( \vec{e_1} ), f ( \vec{e_2} ) \right) = \left( \begin{array}{ccc} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \right)
\]となります。

回転行列は直交行列となっています。

回転行列を用いることで、元の座標を \( (x,y) \) 、原点中心に \( \theta \) 回転させた座標を \( (x',y') \) とすると、\[\begin{align*}
\left( \begin{array}{ccc} x' \\ y' \end{array} \right) & = \left( \begin{array}{ccc} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \right) \left( \begin{array}{ccc} x \\ y \end{array} \right)
\\ & = \left( \begin{array}{ccc} x \cos \theta - y \sin \theta \\ x \sin \theta + y \cos \theta \end{array} \right)
\end{align*} \]と表すことができます。

スポンサードリンク

２．回転変換（3次元回転行列）

先ほど説明した2次元の回転変換を3次元の場合に拡張して考えてみましょう。
2次元の場合と同様に求めることができます。

しかし、3次元の場合は回転する軸（\( x \) 軸回り、\( y \) 軸回り、\( z \) 軸回りの3つ）によって合計3パターンの回転行列が存在します。

いずれの3パターンの場合でも表現行列を求める際には、3次元標準基底\[
\vec{e_1} = \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right) , \ \ \
\vec{e_2} = \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \end{array} \right) , \ \ \
\vec{e_3} = \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \end{array} \right)
\]の行き先を考えればOKです。

(1) x軸回りの回転

まずは \( x \) 軸回りの回転変換 \( f \) の表現行列 \( R_x( \theta ) \) を求めてみましょう。

\( x \) 軸回りの回転なので \( x \) 軸方向の単位ベクトルを表す \( \vec{e_1} \) は変換の前後で向きが変化しませんね。なので、\[
f ( \vec{e_1} ) = \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right)
\]となります。

残りの \( \vec{e_2} \), \( \vec{e_3} \) はそのまま考えるのは少しむずかしいので、\( x \) の正の方向からみた \( yz \) 座標平面を書いて変換の前後でどのようにベクトルが変わるのかを考えることをおすすめします*2。

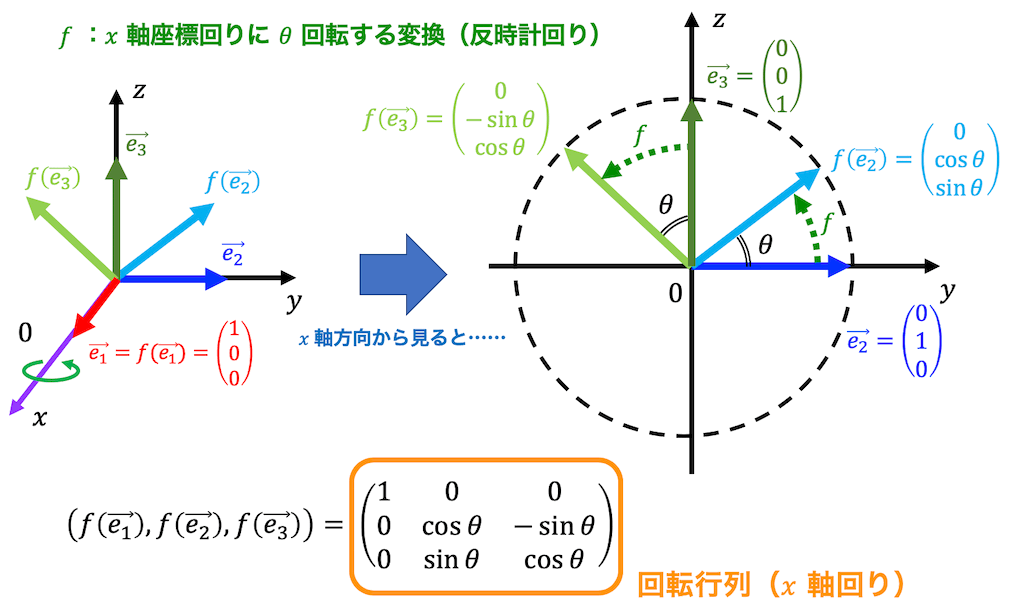
上のように図示すると、2次元の場合と同じような要領で\[
f ( \vec{e_2} ) = \left( \begin{array}{ccc} 0 \\ \cos \theta \\ \sin \theta \end{array} \right) \\
f ( \vec{e_3} ) = \left( \begin{array}{ccc} 0 \\ - \sin \theta \\ \cos x \end{array} \right)
\]を求めることができます。

よって、 \( x \) 軸回りに \( \theta \) 回転する変換 \( f \) の表現行列 \( R_x( \theta) \) は、\[ \begin{align*}
R_x( \theta) & = \left( f ( \vec{e_1} ), f ( \vec{e_2} ) , f( \vec{e_3}  \right)
\\ & = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \theta & - \sin \theta \\ 0 & \sin \theta & \cos \theta \end{array} \right)
\end{align*} \]と求められます。

(2) y軸回りの回転

\( y \) 軸回りの回転変換 \( f \) の表現行列 \( R_y( \theta ) \) も(1)と同様に求められます。

\( y \) 軸回りの回転なので \( y \) 軸方向の単位ベクトルを表す \( \vec{e_2} \) は変換の前後で向きが変化しませんね。なので、\[
f ( \vec{e_2} ) = \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \end{array} \right)
\]となります。

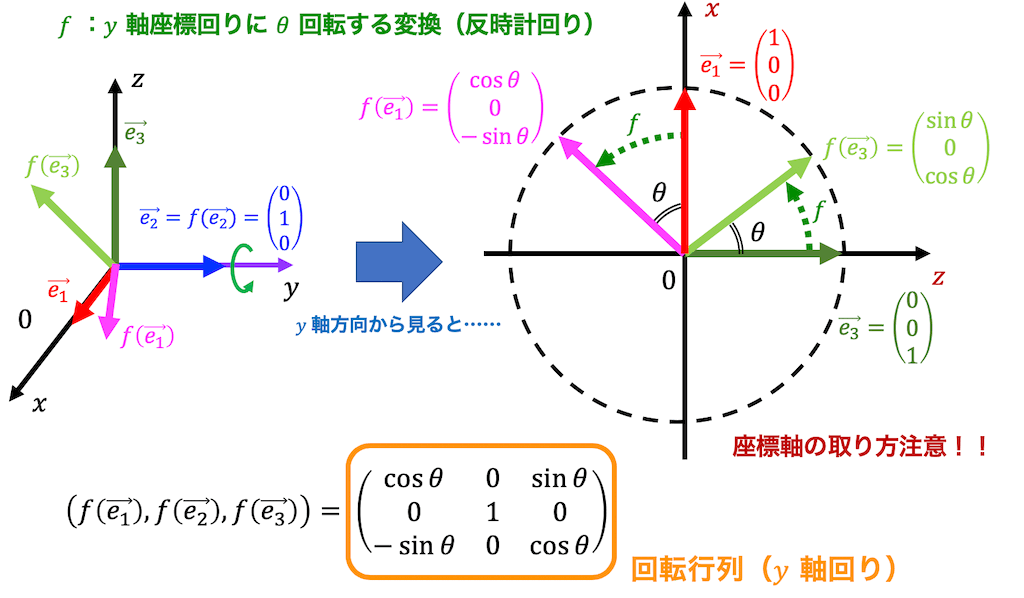
残り2つのベクトルは(1)と同じように \( y \) の正の方向から見た \( zx \) 平面を書くことで動きがわかりやすくなります。

※\( z \), \( x \) の順番に注意してください。

よって、残りの2つのベクトルも\[
f ( \vec{e_1} ) = \left( \begin{array}{ccc} \cos \theta \\ 0 \\ - \sin \theta \end{array} \right) \ \ \
f ( \vec{e_3} ) = \left( \begin{array}{ccc}\sin \theta \\ 0 \\ \cos \theta \end{array} \right)
\]と求められます。

よって、 \( y \) 軸回りに \( \theta \) 回転する変換 \( f \) の表現行列 \( R_y( \theta) \) は、\[ \begin{align*}
R_y( \theta) & = \left( f ( \vec{e_1} ), f ( \vec{e_2} ) , f( \vec{e_3}  \right)
\\ & = \left( \begin{array}{ccc} \cos \theta & 0 & \sin \theta \\ 0 & 1 & 0 \\ - \sin \theta & 0 & \cos \theta \end{array} \right)
\end{align*} \]と求められます。

(3) z軸回りの回転

\( z \) 軸回りの回転変換 \( f \) の表現行列 \( R_z( \theta ) \) も(1)と同様に求められます。

\( z \) 軸回りの回転なので \( z \) 軸方向の単位ベクトルを表す \( \vec{e_2} \) は変化なし、よって\[
f ( \vec{e_3} ) = \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \end{array} \right)
\]となります。

残り2つのベクトルも(1),(2)と同じように \( x \) の正の方向から見た \( xy \) 平面を書くとすぐわかります。

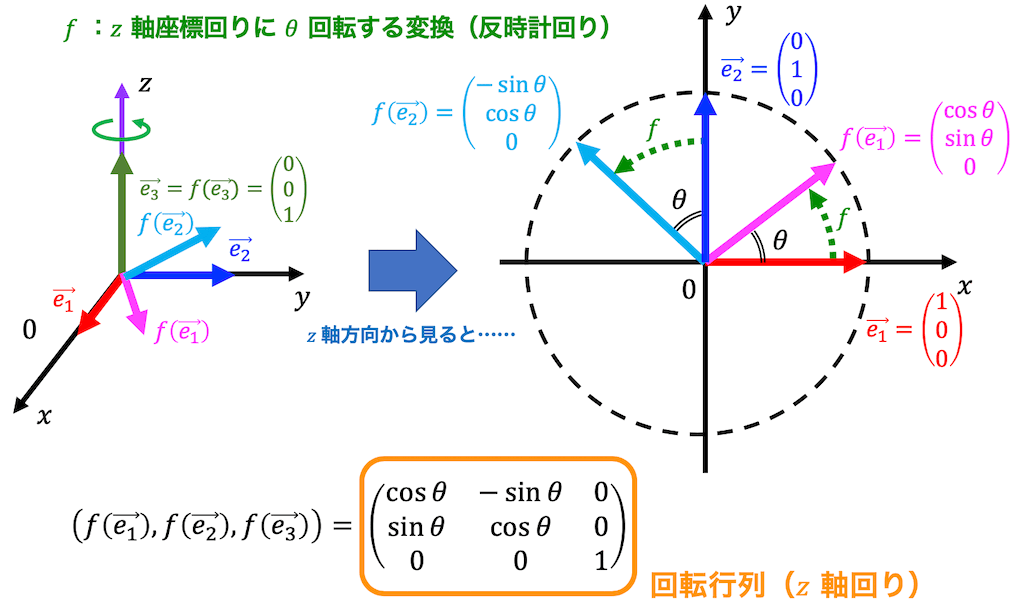
残りの2つのベクトルは\[
f ( \vec{e_1} ) = \left( \begin{array}{ccc} \cos \theta \\ \sin \theta \\ 0 \end{array} \right) \ \ \
f ( \vec{e_2} ) = \left( \begin{array}{ccc} - \sin \theta \\ \cos \theta \\ 0 \end{array} \right)
\]と求められます。

よって、 \( z \) 軸回りに \( \theta \) 回転する変換 \( f \) の表現行列 \( R_z( \theta) \) は、\[ \begin{align*}
R_z( \theta) & = \left( f ( \vec{e_1} ), f ( \vec{e_2} ) , f( \vec{e_3}  \right)
\\ & = \left( \begin{array}{ccc} \cos \theta & - \sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{array} \right)
\end{align*} \]と求められます。

3次元の場合でも回転行列は直交行列となります。

(4) ロドリゲスの回転公式（おまけ）

任意の軸回りの回転変換 \( f \) を表す表現行列を参考までに紹介しておきます。

任意の軸 \[
\vec{n} = \left( n_x , n_y , x_z  \right)
\]回りの回転を表す回転行列は、

\[
R_n (\theta )= \begin{pmatrix}
n_{x}^{2} \left( 1- \cos\theta \right) + \cos \theta & n_{x}n_{y} \left( 1- \cos\theta \right) - n_{z} \sin \theta & n_{x}n_{z} \left( 1- \cos \theta \right) + n_{y} \sin \theta \\
n_{y}n_{x} \left( 1- \cos\theta \right) + n_{z} \sin\theta & n_{y}^{2} \left( 1- \cos\theta \right) +\cos \theta & n_{y}n_{z} \left( 1- \cos\theta \right) - n_{x} \sin \theta \\
n_{z}n_{x} \left( 1- \cos\theta \right) - n_{y}\sin\theta & n_{z}n_{y} \left( 1- \cos\theta \right) + n_{x}\sin\theta &  n_{z}^{2}\left( 1- \cos\theta \right) + \cos \theta \\
\end{pmatrix}
\]

と表せます（ロドリゲスの回転公式、ロドリゲスの定理と呼ばれます）。

スポンサードリンク

３．対称変換

原点を通るような直線 \( l \ : \ y = ax \) に関する対称移動を表す線形変換 \( f \) の表現行列を考えてみましょう。

直線 \( l \) の傾き \( a \) は、\( x \) 軸と \( l \) のなす角 \( \theta \) を用いて、\[
a = \tan \theta
\]と表すことができます。つまり、\[
y = ( \tan \theta )x
\]に関する対称移動を求めればいいことになります。

今まで通り2次元標準基底\[
\vec{e_1} = \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right) , \ \ \
\vec{e_2} = \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right)
\]の行き先を考えることで表現行列を求めていきます。

\( \vec{e_1} \) 、\( \vec{e_2} \) を対称移動させた様子を図示すると、下のようになります。

[修正] \( \beta =  \alpha - 2 \theta\) と書かれている部分は、正しくは \( \beta = \alpha - \theta \) です。

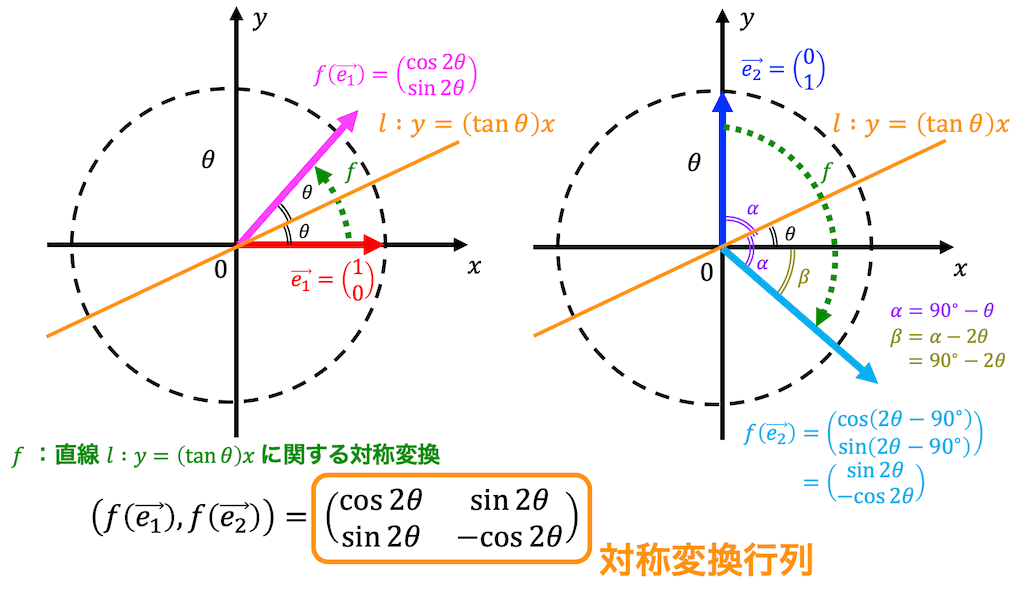
\( \vec{e_1} \) から \( f( \vec{e_1} ) \) への変換は比較的わかりやすいと思います。\[
f( \vec{e_1} ) = \left( \begin{array}{ccc} \cos 2 \theta \\ \sin 2 \theta \end{array} \right)
\]となります。

\( \vec{e_2} \) から \( \vec{e_2} \) への変換が少しわかりにくいかもしれません。

図のように \( \alpha \), \( \beta \) を取ると、\( \vec{e_2} \) から \( f( \vec{e_2} ) \) に変換する際に \( 2 \alpha \) 時計回りに回転していることがわかると思います。

\( 0^{\circ} \) 以降の回転している部分を \( \beta \) とすると、\( \alpha = 90^{\circ} - \theta \) なので、\[\begin{align*}
\beta & = \alpha - \theta
\\ & = (90^{\circ} -  \theta) - \theta
\\ & = 90^{\circ} - 2 \theta
\end{align*}\]と計算できます。

時計回りに \( \beta \) 回転しているということは、反時計回りには \( - \beta \) 回転しているので、\( \vec{e_2} \) は、\[ \begin{align*}
f( \vec{e_2} ) & = \left( \begin{array}{ccc} \cos (2 \theta - 90^{\circ}) \\ \sin (2 \theta - 90^{\circ}) \end{array} \right)
\\ & = \left( \begin{array}{ccc} \sin 2 \theta  \\ - \cos 2 \theta \end{array} \right)
\end{align*} \]と求められます*3。

よって直線 \( l \  y = ( \tan \theta ) x \) に関する対称移動を表す線形変換 \( f \) の表現行列 \( S( \theta ) \) は、\[
S(\theta) = \left( f ( \vec{e_1} ), f ( \vec{e_2} ) \right) = \left( \begin{array}{ccc} \cos 2 \theta &  \sin 2 \theta \\ \sin 2  \theta & -  \cos 2 \theta \end{array} \right)
\]となります。

対称変換行列も回転行列と同様に直交行列となります。

対称変換行列を用いることで、元の座標を \( (x,y) \) 、直線 \( l \  y = ( \tan \theta ) x \) に関する対称移動後の座標を \( (x',y') \) とすると、\[\begin{align*}
\left( \begin{array}{ccc} x' \\ y' \end{array} \right) & = \left( \begin{array}{ccc} \cos 2 \theta &  \sin 2 \theta \\ \sin 2  \theta & -  \cos 2 \theta \end{array} \right)  \left( \begin{array}{ccc} x \\ y \end{array} \right)
\\ & = \left( \begin{array}{ccc} x \cos 2 \theta +  y \sin 2 \theta \\ x \sin 2 \theta - y \cos  2 \theta \end{array} \right)
\end{align*} \]と表すことができます。

４．練習問題

では、簡単にですが、練習をしてみましょう。

練習1

2次元ベクトル空間において、つぎの(1)～(5)が示す対称移動の線形変換行列を求め、①～⑥の中から選びなさい。

(1) \( x \) 軸に関する対称移動
(2) \( y \) 軸に関する対称移動
(3) 原点に関する対称移動
(4) \( y = x \) に関する対称移動
(5) \( y = -x \) に関する対称移動

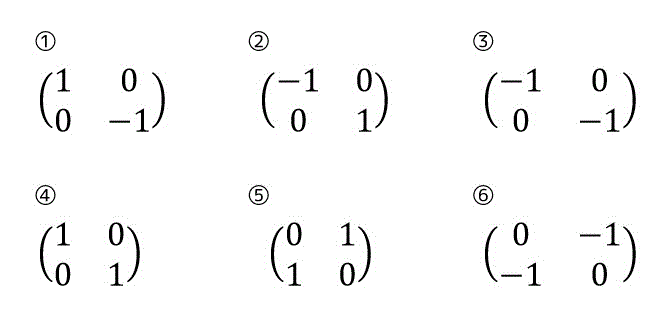
練習2

2次元ベクトル空間上における点A (6,4) を(1),(2)の方法で移動させた点の座標を求めなさい。

(1) 原点中心に \( 30^{\circ} \) 回転させた点Bの座標
(2) 直線 \( y = 2x \) について対称移動させた点Cの座標

５．練習問題の答え

解答1

(1) \( x \) 軸に関する対称移動

正解：①

\( \theta = 0^{\circ} \) のときの直線 \( y = ( \tan \theta ) x \) に関する対称移動と同じ。

なので、\[
S(\theta) = \left( \begin{array}{ccc} \cos 0^{\circ} &  \sin 0^{\circ} \\ \sin 0^{\circ} & -  \cos 0^{\circ} \end{array} \right) = \left( \begin{array}{ccc} 1 &  0 \\ 0 & -1 \end{array} \right)
\]となる。

(2) \( y \) 軸に関する対称移動

正解：②

\( \theta = 90^{\circ} \) のときの直線 \( y = ( \tan \theta ) x \) に関する対称移動と同じ。

なので、\[
S(90^{\circ}) = \left( \begin{array}{ccc} \cos 180^{\circ} &  \sin 180^{\circ} \\ \sin 180^{\circ} & -  \cos 180^{\circ} \end{array} \right) = \left( \begin{array}{ccc} -1 &  0 \\ 0 & 1 \end{array} \right)
\]となる。

(3) 原点に関する対称移動

正解：③

やり方は2パターン

[パターン1：合成変換を利用]

原点に関する対称移動は、\( x \) 軸に関する対称移動 → \( y \) 軸に関する対称移動の2つの操作で実現できる。

よって、原点に関する対称変換行列は \( y \) 軸に関する対称移動と \( x \) 軸に関する対称移動の積で求められる*4。

よって、\[
\left( \begin{array}{ccc} -1 &  0 \\ 0 & 1 \end{array} \right) \left( \begin{array}{ccc} 1 &  0 \\ 0 & -1 \end{array} \right) = \left( \begin{array}{ccc} -1 &  0 \\ 0 & -1 \end{array} \right)
\]と求められる。

[パターン2：回転行列を利用]

原点に関する対称移動は、原点中心に \( 180^{\circ} \) 回転させた移動と同じ。

よって、\[
R(180^{\circ}) = \left( \begin{array}{ccc} \cos 180^{\circ} & - \sin 180^{\circ} \\ \sin 180^{\circ} & \cos 180^{\circ} \end{array} \right)
= \left( \begin{array}{ccc} -1 & 0 \\ 0 & -1 \end{array} \right)
\]と求められる。

(4) \( y = x \) に関する対称移動

正解：⑤

\( \theta = 45^{\circ} \) のときの直線 \( y = ( \tan \theta ) x \) に関する対称移動と同じ。

なので、\[
S(45^{\circ}) = \left( \begin{array}{ccc} \cos 90^{\circ} &  \sin 90^{\circ} \\ \sin 90^{\circ} & -  \cos 90^{\circ} \end{array} \right) = \left( \begin{array}{ccc} 0 &  1 \\ 1 & 0 \end{array} \right)
\]となる。

(5) \( y = -x \) に関する対称移動

正解：⑥

\( \theta = -45^{\circ} \) のときの直線 \( y = ( \tan \theta ) x \) に関する対称移動と同じ。

なので、\[
S(-45^{\circ}) = \left( \begin{array}{ccc} \cos -90^{\circ} &  \sin -90^{\circ} \\ \sin -90^{\circ} & -  \cos -90^{\circ} \end{array} \right) = \left( \begin{array}{ccc} 0 &  -1 \\ -1 & 0 \end{array} \right)
\]となる。

解答2

(1)

原点中心に \( 30^{\circ} \) 回転させる表現行列 \( R( 30^{\circ}) \) は、\[
R( 30^{\circ}) = \left( \begin{array}{ccc} \cos 30^{\circ} & - \sin 30^{\circ} \\ \sin 30^{\circ} & \cos 30^{\circ} \end{array} \right)
= \left( \begin{array}{ccc} \frac{ \sqrt{3} }{2} & - \frac{1}{2} \\ \frac{1}{2} & \frac{ \sqrt{3} }{2} \end{array} \right)
\]となる。

よって座標 \( B \) は、\[
\left( \begin{array}{ccc} \frac{ \sqrt{3} }{2} & - \frac{1}{2} \\ \frac{1}{2} & \frac{ \sqrt{3} }{2} \end{array} \right) \left( \begin{array}{ccc} 6 \\ 4 \end{array} \right) = \left( \begin{array}{ccc} 3 \sqrt{3} - 2 \\ 2 \sqrt{3} + 3 \end{array} \right)
\]となる。

(2)

直線 \( l \) の傾きが2のときの \( x \) 軸と \( l \) がなす角度は、\[
\tan \theta = 2
\]となるので、\[
\cos 2 \theta = \frac{1 - \tan^2 \theta}{1 + \tan^2 \theta} = - \frac{3}{5} \\
\sin 2 \theta = \frac{2 \tan \theta}{1 + \tan^2 \theta} = \frac{4}{5}
\]となる*5。

よって、(2)の変換を表す行列は\[ \begin{align*}
S & = \left( \begin{array}{ccc} - \frac{3}{5} &  \frac{4}{5} \\ \frac{4}{5} & \frac{3}{5}  \end{array} \right)
\\ & =  \frac{1}{5} \left( \begin{array}{ccc} -3 & 4 \\ 4 & 3  \end{array} \right)
\end{align*} \]となる。

よって座標Cは、\[
\frac{1}{5} \left( \begin{array}{ccc} -3 & 4 \\ 4 & 3  \end{array} \right) \left( \begin{array}{ccc} 6 \\ 4 \end{array} \right)
= \frac{1}{5} \left( \begin{array}{ccc} -2 \\ 36 \end{array} \right)
\]となる。

６．さいごに

今回は行列の2次元・3次元の回転変換、対称変換についてまとめました。

練習問題では3次元の回転変換の問題を用意していませんが、もし必要な方は個人で3次元の回転変換の問題を解いていきましょう。

ちなみに、2次の直交行列は、回転を表す行列\[
R(\theta) = \left( \begin{array}{ccc} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \right)\]もしくは、対称変換を表す行列 \[
S( \theta / 2) = \left( \begin{array}{ccc} \cos \theta &  \sin \theta \\ \sin \theta & - \cos \theta \end{array} \right)
\]（\( 2 \theta \to \theta \) に変えている）

の2パターンしかないことを頭に入れておくとどこかで役にたつかもしれません。