Web Analytics Made Easy - StatCounter

工業大学生ももやまのうさぎ塾

うさぎでもわかるをモットーに大学レベルの数学・情報科目をわかりやすく解説！

トップ > 数学 > うさぎでもわかる線形代数　第21羽　2次形式の応用・2次曲線のグラフ

うさぎでもわかる線形代数　第21羽　2次形式の応用・2次曲線のグラフ

数学 数学-大学数学 数学-大学数学-線形代数 まとめシリーズ

こんにちは、ももやまです。
今回は、前回まとめた2次形式の標準形の変換を応用して、2次曲線のグラフを書いてみる方法を紹介しましょう！

 

 

前回の記事（2次形式）についてはこちら！

www.momoyama-usagi.com

※2次形式の知識を使っていくのでまだよくわかってない人は復習しましょう。

 

１．2次曲線の基礎

2次曲線とは、\[
a x^2 + 2p xy + by^2 + 2qx + 2ry + c = 0
\]で表されるような曲線のことをいいます*1。

2次曲線の式の係数部分（ a, b, c, p, q, r）を変えることにより、点、直線、放物線、円、楕円、双曲線などの様々な図形を表現することができます。

点、直線、円の概形に関しては高校数学（数1,2）で習ったで特に復習しません。もし忘れてしまった人はすぐ思い出しましょう。

 

楕円、双曲線、放物線については数3（数C？）で習ったと思うのですが、まだ習っていない（or忘れてしまった）人もいると思うので、少しだけ概形の説明をしたいと思います。

 

２．おもな図形の標準形

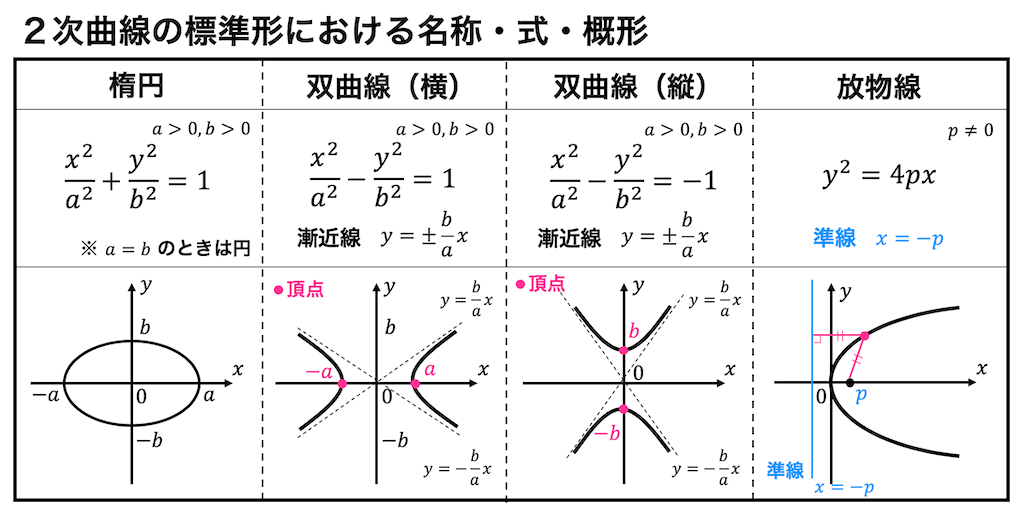
下のほうに楕円、双曲線、放物線の数式、概形を示したので確認してください。 

f:id:momoyama1192:20190830211950g:plain

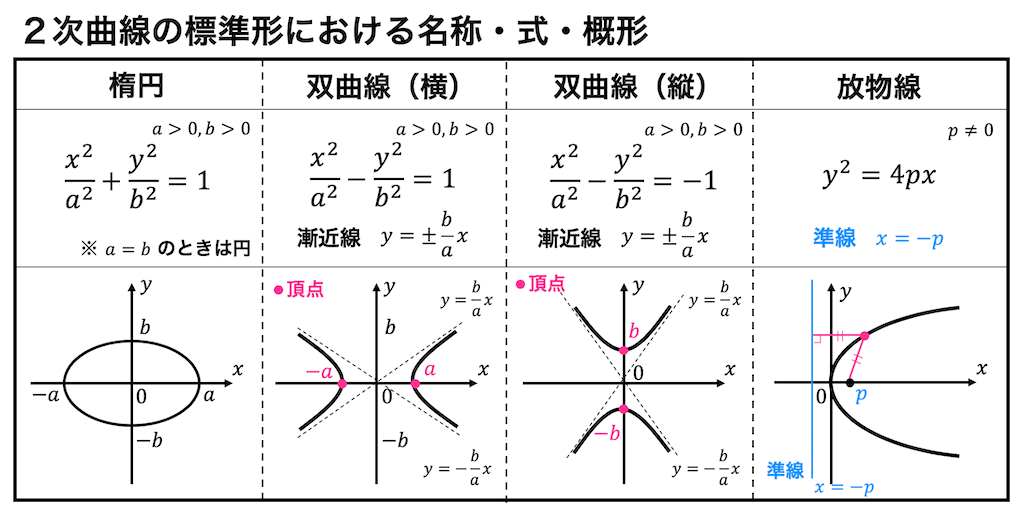
2次曲線のグラフを2次形式の知識を用いて書く問題はたいていこの4パターンのいずれかに落ち着きます。

 

（4パターンに限らず、すべての）2次曲線の標準形と図形の名称を下に記します。

   

2次曲線の標準形と名称

2次曲線の標準形には、

楕円： ax^2 + by^2 = 1
双曲線： ax^2 - by^2 = \pm 1
虚楕円： -ax^2 - by^2 = 1（図書けない）
１点： ax^2 + by^2 = 0
交差する２直線： ax^2 - by^2 = 0
平行な２直線： ax^2 = 1
虚平行な２直線： ax^2 = 1（図書けない）
重複する１直線： ax^2 = 0
放物線： x^2 = 4ay

がある。（ただし a \gt 0, b \gt 0）

※すべてを覚える必要はありません。楕円、双曲線、放物線の３つを覚えておけば十分です！

 

また、2次形式が楕円・双曲線・放物線のいずれかのとき、次の式が成立します。

   

２次形式と名称の関係

2次曲線\[
a x^2 + 2p xy + by^2 + 2qx + 2ry + c = 0
\]が

楕円のとき： ab - p^2 \gt 0
双曲線のとき： ab - p^2 \lt 0 
放物線のとき： ab - p^2 = 0

が成立する。

※ただし逆（ ab - p^2 \gt 0 ならば楕円）は成立するとは限らないので注意！
（例えば 5x^2 + 4y^2 + 1 = 0 は ab - p^2 = 20 \gt 0 となるが楕円とはならない、というかそもそも図形が書けない。）

 

３．2次形式の標準形を用いた2次曲線のグラフの書き方

例題を1つ用意しました。
この例題を用いて2次曲線のグラフの書き方を説明していきましょう。

例題1

つぎの2次曲線\[
5x^2 - 2xy + 5y^2 -12x + 12y + 10 = 0
\]について、次の問いに答えなさい。

(1) 2次形式 \[
5x^2 - 2xy + 5y^2
\]の標準形を求めなさい。

(2) 2次形式\[
5x^2 - 2xy + 5y^2 -12x + 12y + 10=0
\]の標準系を求めなさい。

(3) 2次曲線のグラフを書きなさい。

 

解説1

(1)から順番に解いていきます。
誘導がグラフを書くための助けとなっています。

 

(1)

Step1：2次形式の主要部分を表現する行列を求める

まずは、数式の中で、 x, y の2次形式になっている部分に注目します。

f:id:momoyama1192:20190830211954g:plain

x, y の2次形式で表されている部分を主要部分と呼ぶことにします。

行列 A 、ベクトル \vec{x} をそれぞれ\[
A = \left( \begin{array}{ccc} 5 & -1 \\ -1 & 5  \end{array} \right) \ \ \ \vec{x} = \left( \begin{array}{ccc} x \\ y  \end{array} \right)
\]とすると2次形式の主要部分を\[
5x^2 - 2xy + 5y^2 =  {}^t\! \vec{x} A \vec{x} 
\]と変形できます。

 

Step2：行列の固有値・固有ベクトルを求め、標準形に

このステップは第20羽で説明した2次形式と全く同じ流れです。
ただし、固有ベクトルをうまく設定しないと*2、後ほどグラフを書く際に苦戦するため注意しましょう（下のほうで改めて説明します）。

行列 A の固有値を t とすると、固有方程式は、\[\begin{align*}
|A-tE| = & \left| \begin{array}{ccc} 5 & -1 \\ -1 & 5  \end{array} \right|
\\ = & (5-t)^2 - 1
\\ = & t^2 - 10t + 24
\\ = & (t-4)(t-6) = 0
\end{align*} \]より固有値は4, 6となる。

 

(i) 固有値が4のとき\[ \begin{align*}
(A-4E) = &
\left( \begin{array}{ccc} 1 & -1 \\ -1 & 1  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1 & 1 \\ 0 & 0  \end{array} \right)
\end{align*} \]となる。\[
x - y = 0
\]を解くと、任意定数 k を用いて\[
\left( \begin{array}{ccc} x \\ y  \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
\]と表せる。

固有ベクトル \vec{p_1} は大きさを1に正規化したベクトル、\[
\vec{p_1} = \frac{1}{\sqrt{2}}\left( \begin{array}{ccc} 1 \\ 1  \end{array} \right)
\]となる。

 

(ii) 固有値が6のとき\[ \begin{align*}
(A-6E) = &
\left( \begin{array}{ccc} -1 & -1 \\ -1 & -1  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1 & 1 \\ 0 & 0  \end{array} \right)
\end{align*} \]となる。\[
x + y = 0
\]を解くと、任意定数 k を用いて\[
\left( \begin{array}{ccc} x \\ y  \end{array} \right) = k \left( \begin{array}{ccc} -1 \\ 1 \end{array} \right)
\]と表せる。

固有ベクトル \vec{p_1} は大きさを1に正規化したベクトルなので、\[
\vec{p_1} = \frac{1}{\sqrt{2}}\left( \begin{array}{ccc} -1 \\ 1  \end{array} \right)
\]となる。

 

\vec{p_1}, \vec{p_2} は正規直交基底となるので、直交行列\[
P = \left( \vec{p_1}, \vec{p_2} \right) = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 & -1 \\ 1 & 1 \end{array} \right) 
\]を用いて、\[
P^{-1} AP = \left( \begin{array}{ccc} 4 & 0 \\ 0 & 6  \end{array} \right) = D
\]と対角化できる。

 

よって、 X, Y を\[
\vec{y} = \left( \begin{array}{ccc} X \\ Y  \end{array} \right) =   {}^t\! P \left( \begin{array}{ccc} x \\ y  \end{array} \right) = {}^t\! P \vec{x}
\]とおくことで、\[
4 X^2 + 6 Y^2
\]と標準形を求められる。

 

(2)

Step3：主要部以外の部分もX,Yに表現する

主要部分を X, Y で表現することができたので、残りの  -12x + 12y + 10 も X, Y に直していきます。

\vec{x} = P \vec{y} なので、\[\begin{align*}
\left( \begin{array}{ccc} x \\ y  \end{array} \right) & = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 & -1 \\ 1 & 1 \end{array} \right) \left( \begin{array}{ccc} X \\ Y  \end{array} \right)
\\ & = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} X - Y \\ X + Y  \end{array} \right)
\end{align*} \]

となるので、\[
x = \frac{ \sqrt{2} }{2} ( X - Y) \\
y = \frac{ \sqrt{2} }{2} ( X + Y)
\]となる。

f:id:momoyama1192:20190830211958g:plain

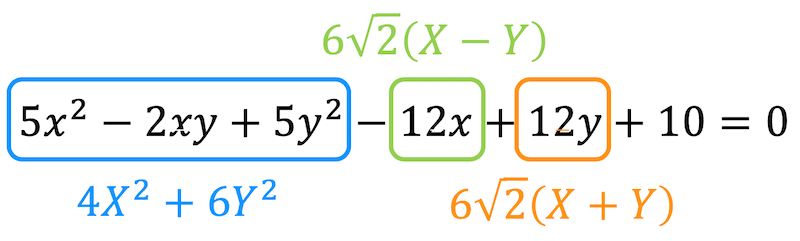
よって、\[ \begin{align*} &
5x^2 - 2xy + 5y^2 -12x + 12y + 10
\\ = & 4 X^2 + 6 Y^2 - 12 \cdot \frac{ \sqrt{2} }{2} ( X - Y) + 12 \cdot \frac{ \sqrt{2} }{2} ( X + Y) + 10
\\ = & 4 X^2 + 6 Y^2 - 6 \sqrt{2} ( X - Y ) + 6 \sqrt{2}  ( X + Y) + 10
\\ = & 4 X^2 + 6 Y^2 + 12 \sqrt{2} Y + 10
\\ = & 4 X^2 + 6 Y^2 + 12 \sqrt{2} Y + 10
\\ = & 4 X^2 + 6 (Y + \sqrt{2})^2 -2 = 0
\end{align*}\]と変形できる。

 

 

Step4：式全体を標準形に（=1の形に）

よって、\[
4 X^2 + 6 (Y + \sqrt{2})^2 = 2 
\]と変換できるので標準形（= 1の形）は、\[
2 X^2 + 3 (Y + \sqrt{2})^2 = 1
\]となる。

 

(3)

Step5：標準形の図形の意味を考える

つぎに求めた標準形がどんな図形なのかを考えましょう\[
2 X^2 + 3 (Y + \sqrt{2})^2 = 1 \\
\frac{X^2}{\left( \frac{ \sqrt{2} }{2} \right)^3} + \frac{Y^2}{\left( \frac{\sqrt{3}}{3} \right)^3}
\]は、 X 軸方向の長さ（長軸）が \frac{\sqrt{2}}{2} \times 2、 Y 軸方向の長さ（短軸）が \frac{\sqrt{3}}{3} \times 2 の楕円（中心 (0,-\sqrt{2}) ですね。

 

Step6：変換P（回転変換）を使い、グラフを図示する

ここで X,Y で表された式から x,y の式に変換するためには行列 P を使いましたね。（ \vec{x} = P \vec{y} ）

この行列 P は\[
P = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 & -1 \\ 1 & 1 \end{array} \right)
\]でしたね。

この行列 P の変換、実は回転行列\[
\left( \begin{array}{ccc} \cos \theta & - \sin \theta \\  \sin \theta & \cos \theta \end{array} \right)
\]の \theta = 45^{\circ} と同じ値*3になるので、行列 P は原点中心に図形を反時計回りに45°回転させる変換とわかります。

 

（今回は \sin \theta, \cos \theta の値が簡単なのですぐに45°回転とわかるのですが、中途半端な値のときは\[
\frac{ \sin \theta }{ \cos \theta } = \tan \theta
\]で \tan \theta を出してからどれくらい回転しているかを把握しましょう。*4。）

 

行列を用いた回転変換を忘れてしまった（orよくわかっていない人）はこちらの記事で復習をしましょう。

www.momoyama-usagi.com

 

また、回転変換をすると図形の中心の位置も変わりますね。変換後の図形の中心は\[
\frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 & -1 \\ 1 & 1 \end{array} \right) \left( \begin{array}{ccc} 0 \\ - \sqrt{2} \end{array} \right) = \left( \begin{array}{ccc} 1 \\ -1 \end{array} \right) 
\]と計算できるので、\[
5x^2 - 2xy + 5y^2 -12x + 12y + 10=0
\]は、中心が (1,-1) の長軸が \sqrt{2}、短軸が \frac{2 \sqrt{3}}{3} を反時計回りに45°傾けた楕円となります。

 

よって、グラフを図示すると下のようになります。
（青色が答え、赤色は変換 P を適用する前のグラフ）

変換 P は、固有ベクトルによって決まります。そのため、なるべくうまくかつ単純な回転になるように固有ベクトルを求めましょう。例えば、上の例題の固有ベクトルを\[
\vec{p_1} = \frac{1}{\sqrt{2}}\left( \begin{array}{ccc} 1 \\ 1  \end{array} \right) \ \ \ \vec{p_2} = \frac{1}{\sqrt{2}}\left( \begin{array}{ccc} 1 \\ -1  \end{array} \right)
\]としてしまうと、\[\begin{align*}
\frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 & 1 \\ 1 & -1 \end{array} \right)  = \left( \begin{array}{ccc} \cos \theta  & - \sin \theta \\ \sin \theta & \cos \theta  \end{array} \right)
\end{align*} \]を満たすような \theta が存在しないため、回転変換ではなくなってしまいます。

４．練習問題

では、1問だけですが練習してみましょう。

 

練習

つぎの2次曲線\[
x^2 - 2 \sqrt{3} xy - y^2 + 4 \sqrt{3} x + 4y + 4 = 0
\]について、次の問いに答えなさい。

(1) 2次形式の主要部分 \[
x^2 - 2 \sqrt{3} xy - y^2
\]の標準形を求めなさい。

(2) 2次形式\[
x^2 - 2 \sqrt{3} xy - y^2 + 4 \sqrt{3} x + 4y + 4 = 0
\]の標準系を求めなさい。

(3) 2次曲線のグラフを書きなさい。

 

５．練習問題の答え 

解答

(1)

Step1：主要部分を表現する行列を求める

誘導の通り、主要部分の2次形式を表現する行列を考える。

行列 A 、ベクトル \vec{x} をそれぞれ\[
A = \left( \begin{array}{ccc} 1 & -\sqrt{3} \\ -\sqrt{3} & -1  \end{array} \right) \ \ \ \vec{x} = \left( \begin{array}{ccc} x \\ y  \end{array} \right)
\]とすると2次形式の主要部分を\[
x^2 - 2 \sqrt{3} xy - y^2 =  {}^t\! \vec{x} A \vec{x} 
\]と変形できます。

 

Step2：行列の固有値・固有ベクトルを求め、標準形に

このステップは第20羽で説明した2次形式と全く同じ流れです。

行列 A の固有値を t とすると、固有方程式は、\[\begin{align*}
|A-tE| = & \left| \begin{array}{ccc} 1-t & -\sqrt{3} \\ -\sqrt{3} & -1-t  \end{array} \right|
\\ = & (t+1)(t-1) - 3
\\ = & t^2 - 4
\\ = & (t+2)(t-2) = 0
\end{align*} \]より固有値は2, -2となる。

 

つぎに固有ベクトルを求める。

ここで直交行列 P がうまく\[
P = \left( \begin{array}{ccc} \cos \theta  & - \sin \theta^{\circ} \\ \sin \theta & \cos \theta  \end{array} \right)
\]のような回転行列にして P が回転変換になるようにします。

(i) 固有値が-2のとき\[ \begin{align*}
(A+2E) = &
\left( \begin{array}{ccc} 3 & -\sqrt{3} \\ -\sqrt{3} & 1   \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} \sqrt{3} & -1  \\ 0 & 0  \end{array} \right)
\end{align*} \]となる。\[
\sqrt{3} x -  y = 0
\]を解くと、任意定数 k を用いて\[
\left( \begin{array}{ccc} x \\ y  \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ \sqrt{3} \end{array} \right)
\]と表せる。

固有ベクトル \vec{p_1} は大きさを1に正規化したベクトル、\[
\vec{p_1} = \frac{1}{2} \left( \begin{array}{ccc} 1 \\ \sqrt{3}  \end{array} \right)
\]となる。

 

(ii) 固有値が2のとき\[ \begin{align*}
(A-2E) = &
\left( \begin{array}{ccc} -1 & -\sqrt{3} \\ -\sqrt{3} & -3  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1 & \sqrt{3} \\ 0 & 0  \end{array} \right)
\end{align*} \]となる。\[
x + \sqrt{3} y = 0
\]を解くと、任意定数 k を用いて\[
\left( \begin{array}{ccc} x \\ y  \end{array} \right) = k \left( \begin{array}{ccc} -\sqrt{3} \\ 1 \end{array} \right)
\]と表せる。

固有ベクトル \vec{p_2} は大きさを1に正規化したベクトルなので、\[
\vec{p_2} = \frac{1}{2}\left( \begin{array}{ccc} -\sqrt{3} \\ 1  \end{array} \right)
\]となる。

 

\vec{p_1}, \vec{p_2} は正規直交基底となるので、直交行列\[
P = \left( \vec{p_1}, \vec{p_2} \right) = \frac{1}{2} \left( \begin{array}{ccc} 1 & -\sqrt{3}  \\ \sqrt{3} & 1 \end{array} \right) 
\]を用いて、\[
P^{-1} AP = \left( \begin{array}{ccc} -2 & 0 \\ 0 & 2  \end{array} \right) = D
\]と対角化できる。

 

よって、 X, Y を\[
\vec{y} = \left( \begin{array}{ccc} X \\ Y  \end{array} \right) =   {}^t\! P \left( \begin{array}{ccc} x \\ y  \end{array} \right) = {}^t\! P \vec{x}
\]とおくことで、\[
- 2 X^2 + 2 Y^2
\]と標準形を求められる。

 

(2)

Step3：主要部以外の部分もX,Yに表現する

主要部分を以外の残りの 4 \sqrt{3} x + 4y + 4 も X, Y に直す。

\vec{x} = P \vec{y} なので、\[\begin{align*}
\left( \begin{array}{ccc} x \\ y  \end{array} \right) & = \frac{1}{2} \left( \begin{array}{ccc} 1 & \sqrt{3}  \\ - \sqrt{3} & 1 \end{array} \right) \left( \begin{array}{ccc} X \\ Y  \end{array} \right)
\\ & = \frac{1}{2} \left( \begin{array}{ccc}  X - \sqrt{3} Y \\ \sqrt{3} X + Y  \end{array} \right)
\end{align*} \]

となるので、\[
x = \frac{ 1 }{2} ( X - \sqrt{3} Y) \\
y = \frac{ 1 }{2} (\sqrt{3} X +  Y)
\]となる。

f:id:momoyama1192:20190830212002g:plain

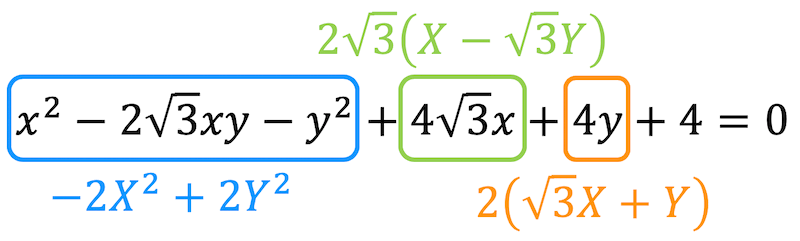
よって、\[ \begin{align*} &
x^2 - 2 \sqrt{3} xy - y^2 + 4 \sqrt{3} + 4y + 4
\\ = & -2 X^2 + 2 Y^2 + 4 \sqrt{3} \cdot \frac{ 1 }{2} ( X - \sqrt{3} Y)+ 4 \cdot \frac{ 1 }{2} (\sqrt{3} X +  Y) + 4
\\ = & -2 X^2 + 2 Y^2 + 2 \sqrt{3} ( X - \sqrt{3} Y)+ 2 ( \sqrt{3} X +  Y) + 4 
\\ = & -2 X^2 + 2 Y^2 + 4 \sqrt{3} X - 4 Y + 4
\\ = & -2(X-\sqrt{3})^2 + 2(Y-1)^2 +8
\end{align*}\]と変形できる。

 

 

Step4：式全体を標準形に（=1の形に）

よって、\[
-2(X-\sqrt{3})^2 + 2(Y-1)^2 = -8 \\
2(X-\sqrt{3})^2 - 2(Y-1)^2 = 8 
\]と変換できるので標準形（= 1の形）は、\[

\frac{(X-\sqrt{3})^2}{4} - \frac{(Y-1)^2}{4} = 1
\]となる。

 

(3)

Step5：標準形の図形の意味を考える

標準形\[
\frac{(X-\sqrt{3})^2}{2^2} - \frac{(Y-1)^2}{2^2} = 1
\]は、頂点 (x,y)= (2,0), (-2,0) を通る漸近線が y = \pm x の双曲線を x 座標方向に \sqrt{3}、 y 座標方向に 1 だけ動かしたものに相当する。
（つまり頂点 (x,y)= (2 + \sqrt{3},1), (-2 + \sqrt{3},1) となる）

 

ここで、標準形の変数 X,Y からもとの変数 x,y への変換は\[
\vec{x} = P \vec{y}
\]と変換行列 P を用いている。この行列 Pは、\[
 \frac{1}{2} \left( \begin{array}{ccc} 1 & -\sqrt{3}  \\ \sqrt{3} & 1 \end{array} \right)  = 
\left( \begin{array}{ccc} \cos 60^{\circ} & - \sin 60^{\circ} \\ \sin 60^{\circ} & \cos 60^{\circ} \end{array} \right) 
\]と、原点中心に反時計回りに 60° 回転する変換を表している。

また、変換Pを行ったときの中心の座標、頂点の座標は下のように計算できる。

中心： (\sqrt{3},1) \to  (0,2) \[
\frac{1}{2} \left( \begin{array}{ccc} 1 & -\sqrt{3}  \\ \sqrt{3} & 1 \end{array} \right)  \left( \begin{array}{ccc} \sqrt{3}  \\ 1 \end{array} \right) = \left( \begin{array}{ccc} 0  \\ 2 \end{array} \right)
\]

頂点1： (2+\sqrt{3},1) \to (1,2 + \sqrt{3}) \[
\frac{1}{2} \left( \begin{array}{ccc} 1 & -\sqrt{3}  \\ \sqrt{3} & 1 \end{array} \right)  \left( \begin{array}{ccc} 2 + \sqrt{3}  \\ 1 \end{array} \right) = \left( \begin{array}{ccc} 1  \\ 2 + \sqrt{3} \end{array} \right)
\]

 

頂点2： (-2+\sqrt{3},1) \to (-1,2 - \sqrt{3}) \[
\frac{1}{2} \left( \begin{array}{ccc} 1 & -\sqrt{3}  \\ \sqrt{3} & 1 \end{array} \right)  \left( \begin{array}{ccc} -2 + \sqrt{3}  \\ 1 \end{array} \right) = \left( \begin{array}{ccc} -1  \\ 2 - \sqrt{3} \end{array} \right)
\]

 

よって、図形の概形（青色が答え、赤色は変換 P 適用前）

となる。

 

おまけ　漸近線も考えてみる

変換 P を適用すると漸近線がどのように変化するのかを見てみましょう。

変換前の漸近線は y = \pm x でしたね。直線の傾きは x 軸と直線がなす角度を \theta とすると、 \tan \theta で傾きを表すことができますね。

今回は y = \pm x なので、漸近線の傾きは 45° と -45° （ \tan 45^{\circ} = 1）ですね。

ここに変換 P を適用するとさらに60°回転するので、漸近線は中心 (0,2) の傾き \tan 105^{\circ} と \tan 15^{\circ} の直線となりますね。それぞれの \tan の値は \[ \begin{align*}
\tan 105^{\circ} & = \tan \left(60^{\circ} + 45^{\circ} \right)
\\  & = \frac{\tan 60^{\circ} + \tan 45^{\circ} }{1 - \tan 60^{\circ} \tan 45^{\circ}  }
\\ & = \frac{\sqrt{3} + 1}{ 1 - \sqrt{3} }
\\ & = -2 -\sqrt{3}
\end{align*} \] \[\begin{align*}
\tan 15^{\circ} & = \tan \left(60^{\circ} - 45^{\circ} \right)
\\  & = \frac{\tan 60^{\circ} - \tan 45^{\circ} }{1 + \tan 60^{\circ} \tan 45^{\circ}  }
\\ & = \frac{\sqrt{3} - 1}{ 1 + \sqrt{3} }
\\ & = 2 - \sqrt{3}
\end{align*} \]となるので、漸近線は\[
y = (2- \sqrt{3})x + 2 \\
y = -(2 + \sqrt{3})x + 2
\]の2本となります。

実際にグラフで確認してみましょう。

たしかに漸近線になっていることがわかります。

 

６．さいごに

今回は2次形式の標準形を利用して、2次曲線のグラフを書く方法についてまとめました。

一見どんな図形かわからない2次曲線も標準形に変換するとで概形を把握することができることがわかりましたね。

 

次回はジョルダン標準形についてまとめていきたいと思います。

*1: p,q,r の係数が1ではなく2になっているのは、2次曲線を x, y, 1 の3変数の2次形式とみたときに {}^t\! \vec{x} A \vec{x} の行列 A, ベクトル \vec{x}の成分が \[
A = \left( \begin{array}{ccc} a & p & q \\ p & b & r \\ q & r & c  \end{array} \right) \ \ \ 
\vec{x} = \left( \begin{array}{ccc} x \\ y \\ 1  \end{array} \right) \] になるようにするため。

*2:2次正方行列の直交行列 P は必ず回転変換か対称変換を表すのですが、対称変換はめんどくさいのでうまく回転変換になるように固有ベクトルを決める必要があります。回転変換にするためには行列 P の行列式が |P| = 1 となるように設定すればOKです。

*3:一応計算すると、\[
\left( \begin{array}{ccc} \cos 45^{\circ} & - \sin 45^{\circ} \\ \sin 45^{\circ} & \cos 45^{\circ} \end{array} \right) = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 & -1 \\ 1 & 1 \end{array} \right) = P
\]となり、たしかに一致する。

*4: \tan \theta は傾きを表すので、標準形と比べてどれくらい傾いているかを簡単に把握することができます。例えば、\[
\sin \theta = \frac{2 \sqrt{5} }{5}, \ \ \ \cos \theta = \frac{  \sqrt{5} }{5}
\]であれば \tan \theta は\[
\tan \theta = \frac{ \sin \theta }{ \cos \theta } = 2
\]となるので、60°ちょいくらい傾いていることがわかりますね。

momoyama1192




スポンサーリンク







スポンサーリンク




コメントを書く