うさぎでもわかる微分方程式　Part11　対角化を用いた連立微分方程式の解き方と指数行列

こんにちは、ももやまです。

今回は、前回に引き続き連立微分方程式について説明していきたいと思います。

今回は、4つの連立微分方程式の解き方

1. 高階（2階以上）微分方程式に変換する方法
2. 行列の対角化・指数行列を用いる方法
3. 微分演算子を用いる方法
4. ラプラス変換を用いる方法（初期値が与えられているとき限定）

の「行列の対角化を用いる方法」について説明していきたいと思います。

前回の微分方程式の記事はこちら！

www.momoyama-usagi.com

スポンサードリンク

１．行列を用いた連立方程式の表現

前回、2元（2つの式の）連立方程式を2階の微分方程式にしてから解く方法について説明しました。

しかし、式が3つ、4つ…と増えたらどうなるでしょう。

高階の微分方程式にするだけでも一苦労ですよね。

そこで、連立微分方程式を行列を用いて表してみましょう。

例えば、2元の連立方程式\[
\left\{ \begin{array}{l} \frac{dx}{dt} = x + 2y \\ \frac{dy}{dt} = 2x + y \end{array}\right.
\]があるとします。

この連立方程式は、\[
\frac{d}{dt} \left( \begin{array}{ccc} x \\ y \end{array} \right) = \left( \begin{array}{ccc} 1 & 2 \\ 2 & 1 \end{array} \right) \left( \begin{array}{ccc} x \\ y \end{array} \right)
\]とすることで行列を用いて表すことができます。

さらに、\[
\vec{x} = \left( \begin{array}{ccc} x \\ y \end{array} \right) , \ \ \ A = \left( \begin{array}{ccc} 1 & 2 \\ 2 & 1 \end{array} \right)
\]とすることで、\[
\frac{d \vec{x} }{dt} = A \vec{x}
\]とコンパクトにまとめることができます。

（このときの行列 \( A \) を係数行列と呼びます。）

スポンサードリンク

２．対角化を用いた連立方程式の解き方

※ もし行列の対角化について忘れてしまった人は下の記事で必ず復習してからご覧ください。

www.momoyama-usagi.com

行列を用いて連立微分方程式\[
\frac{d \vec{x} }{dt} = A \vec{x}
\]を解く際には対角化を行います。

例題1

連立微分方程式\[
\left\{ \begin{array}{l} \frac{dx}{dt} = x + 2y \\ \frac{dy}{dt} = 2x + y \end{array}\right.
\]は、行列を用いて\[
\frac{d}{dt} \left( \begin{array}{ccc} x \\ y \end{array} \right) = \left( \begin{array}{ccc} 1 & 2 \\ 2 & 1 \end{array} \right) \left( \begin{array}{ccc} x \\ y \end{array} \right) \]\[
\frac{d \vec{x} }{dt} = A \vec{x}
\]と表すことができる。(1), (2)の問いに答えなさい。

(1) 行列\[
A = \left( \begin{array}{ccc} 1 & 2 \\ 2 & 1 \end{array} \right)
\]の固有値、固有ベクトルを求め、対角化しなさい。

(2) (1)を用いて連立微分方程式の一般解を求めなさい。

(3) 初期条件\[
\vec{x}(0) = \left( \begin{array}{ccc} x(0) \\ y(0) \end{array} \right) = \left( \begin{array}{ccc} 2 \\ 0 \end{array} \right)
\]における解を求めなさい。

解説1

固有値を \( k \) とすると、固有値は\[\begin{align*}
|A - kE| = 0
\end{align*}\]を満たす \( k \) が固有値となるのでしたね。

早速解いていくと、\[\begin{align*}
|A - tE| & = \left| \begin{array}{ccc} 1-t & 2 \\ 2 & 1-t \end{array} \right|
\\ & = (1-k)^2 - 4
\\ & = k^2 - 2k+ 1 - 4
\\ & = k^2 - 2k - 3
\\ & = (k-3)(k+1)
\\ & = 0
\end{align*}\]と変形できるので、固有値は-1, 3となる。

（固有値の総和は対角成分の総和（今回は2）に等しいことを必ず確認すること！）

つぎに、対応する固有値ごとに固有ベクトルを求める。

対応する固有値 \( k \) の固有ベクトル \( \vec{p} \) は、連立方程式\[
(A - kE) \vec{p} = \vec{0}
\]を解くことで求められる。

(i) 固有値が-1のときの固有ベクトル \( \vec{p}_1 \)

行列 \( A - E \) の変形を行うと、\[\begin{align*}
A - E & = \left( \begin{array}{ccc} 2 & 2 \\ 2 & 2 \end{array} \right) \\ & \to \left( \begin{array}{ccc} 1 & 1 \\ 0 & 0 \end{array} \right)
\end{align*}\]となる。方程式\[
x + y = 0
\]の解は任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ -1 \end{array} \right)
\]となるので、固有ベクトル \( \vec{p}_1 \) は\[
\vec{p}_1 = \left( \begin{array}{ccc} 1 \\ -1 \end{array} \right)
\]となる。

(ii) 固有値が3のときの固有ベクトル \( \vec{p}_3 \)

行列 \( A - 3E \) の変形を行うと、\[\begin{align*}
A - E & = \left( \begin{array}{ccc} -1 & 1 \\ -1 & 1 \end{array} \right) \\ & \to \left( \begin{array}{ccc} 1 & -1 \\ 0 & 0 \end{array} \right)
\end{align*}\]となる。方程式\[
x - y = 0
\]の解は任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
\]となるので、固有ベクトル \( \vec{p}_2 \) は\[
\vec{p}_2 = \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
\]となる。

よって、行列 \( P \) を\[
P = \left( \begin{array}{ccc} \vec{p}_1 \\ \vec{p}_2 \end{array} \right) = \left( \begin{array}{ccc} 1 & 1 \\ -1 & 1 \end{array} \right)
\]とすることで、\[
P^{-1} A P = \left( \begin{array}{ccc} -1 & 0 \\ 0 & 3 \end{array} \right) = D
\]と対角化することができます。

（試験の際には \( AP = PD \) で対角化が正しいかどうかを必ず確認すること！）

(2)

対角化の式\[
P^{-1} AP = D
\]に左辺から \( P \)、右辺から \( P^{-1} \) を掛けると\[\begin{align*}
\color{red}{P} P^{-1} AP \color{blue}{P^{-1}} & = \color{red}{P} D \color{blue}{P^{-1}} \\
A & = P D P^{-1}
\end{align*}\]が成立する。

これを連立方程式\[
\frac{d \vec{x} }{dt} = A \vec{x}
\]に代入すると、\[
\frac{d \vec{x} }{dt} = P D P^{-1} \vec{x}
\]となる。

さらに左辺から \( P^{-1} \) を掛けてあげると、\[\begin{align*}
P^{-1} \frac{d \vec{x} }{dt} & = P^{-1} P D P^{-1} \vec{x}
\\ & = D P^{-1} \vec{x}
\end{align*} \]となる。

ここで、\( P^{-1} \) は定数なので、\[
P^{-1} \frac{d \vec{x} }{dt} = \frac{d}{dt} P^{-1} \vec{x}
\]と微分演算子 \( \frac{d}{dt} \) の中に入れることができる。

よって、\[
\frac{d}{dt} \left( P^{-1} \vec{x} \right) = D P^{-1} \vec{x}
\]が成立する。

※ 対角化後の行列の変形手順をまとめると下のようになります

ここで、\( P^{-1} \vec{x} = \vec{y} \)（つまり \( \vec{x} = P \vec{y} \)）とおくと、\[
\frac{d}{dt} \vec{y} = D \vec{y}
\]と書き換えられる。

成分で表すと、\[
\frac{d}{dt} \left( \begin{array}{ccc} X \\ Y \end{array} \right) = \left( \begin{array}{ccc} -1 & 0 \\ 0 & 3 \end{array} \right) \left( \begin{array}{ccc} X \\ Y \end{array} \right)
\]とかけるので、分離すると\[
\frac{d X}{dt} = -X \ \ \Rightarrow \ \ \frac{1}{X} \frac{d X}{dt} = -1 \]\[
\frac{d Y}{dt} = 3Y \ \ \Rightarrow \ \ \frac{1}{X} \frac{d Y}{dt} = 3
\]となり、変数分離形に持ち込めます。

よって、\( X \), \( Y \) の解は任意定数 \( C_1 \), \( C_2 \) を用いて\[
X = C_1 e^{-t}, \ \ \ Y = C_2 e^{3t}
\]となります。

ここで、\( \vec{x} = P \vec{y} \) なので、\[\begin{align*}
\vec{x} = \left( \begin{array}{ccc} x \\ y \end{array} \right) & = \left( \begin{array}{ccc} 1 & 1 \\ -1 & 1 \end{array} \right) \left( \begin{array}{ccc} X \\ Y \end{array} \right)
\\ & = \left( \begin{array}{ccc} X+Y \\ -X+Y \end{array} \right)
\\ & = \left( \begin{array}{ccc} C_1 e^{-t} + C_2 e^{3t} \\ - C_1 e^{-t} + C_2 e^{3t} \end{array} \right)
\end{align*} \]となり、一般解を\[
\left\{ \begin{array}{l} x = C_1 e^{-t} + C_2 e^{3t} \\ y = - C_1 e^{-t} + C_2 e^{3t} \end{array}\right.
\]と求めることができます。

（ただ一般解を求めるだけであれば逆行列 \( P^{-1} \) の計算は不要！）

(3)

(2)の一般解に \( x(0) = 1 \), \( y(0) = 0 \) を入れて解いてもいいのですが、せっかくなので行列を使って解いてみましょう。

\( t = 0 \) を代入すると、\( \vec{y} (0) \) は \( P^{-1} \vec{x} = \vec{y} \) より\[\begin{align*}
\vec{y}(0) & = \left( \begin{array}{ccc} X(0) \\ Y(0) \end{array} \right)
\\ & = \left( \begin{array}{ccc} C_1 \\ C_2 \end{array} \right)
\\ & =  P^{-1} \vec{x} (0)
\\ & = P^{-1} \left( \begin{array}{ccc} x(0) \\ y(0) \end{array} \right)
\end{align*}\]で表せる。

また、 逆行列 \( P^{-1} \) は、\[
P^{-1} = \frac{1}{2} \left( \begin{array}{ccc} 1 & -1 \\ 1 & 1 \end{array} \right)
\]となるので、\[\begin{align*}
\left( \begin{array}{ccc} C_1 \\ C_2 \end{array} \right)  & = \frac{1}{2} \left( \begin{array}{ccc} 1 & -1 \\ 1 & 1 \end{array} \right) \left( \begin{array}{ccc} 2 \\ 0 \end{array} \right)
\\ & =  \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
\end{align*} \]となる。

よって、一般解は\[
\left\{ \begin{array}{l} x = e^{-t} + e^{3t} \\ y = - e^{-t} + e^{3t} \end{array}\right.
\]となる。

なお、対角化できない行列の場合は例題1のような解き方はできないので注意してください。

（係数行列が対角化できない場合は、下で紹介する指数行列とジョルダン標準形の変形を利用することで一般解を求めます。）

スポンサードリンク

３．指数行列

(1) 指数行列の仕組みと重要な法則

連立微分方程式を行列を用いて\[
\frac{d \vec{x} }{dt} = A \vec{x}
\]と表すこができることを先程説明しましたね。

この式を\[
\frac{1}{ \vec{x} } \frac{d \vec{x} }{dt} = A
\]とすることで任意定数が入ったベクトル \( \vec{c} \) を用いて\[
\vec{x} = e^{At} \vec{c}
\]と表現できないかなぁと思う人もいるかもしれません。

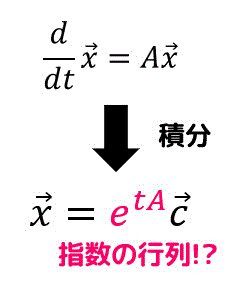
そこで、とある人が \( e \) の行列 \( A \) 乗を\[\begin{align*}
e^A & = E + A + \frac{1}{2!} A^2 + \cdots + \frac{1}{n!} A^n + \cdots
\\ & = \sum^{\infty}_{n = 0} \frac{1}{n!} A^n
\end{align*}\]のようなマクローリン展開の形で定義しました。

この \( e \) の指数に行列 \( A \) を載せた \( e^A \) のことを指数行列と呼びます。

マクローリン展開について忘れてしまった人は下の記事で復習しましょう。

www.momoyama-usagi.com

指数行列には様々な法則が成り立ちますが、その中でも特に重要な5つを紹介しましょう。

法則2を用いることで、連立微分方程式\[
\frac{d}{dt}  \vec{x} = A \vec{x}
\]から、\[
\vec{x} = e^{tA} \vec{c}, \ \ \ \vec{c} = \left( \begin{array}{ccc} C_1 \\ C_2 \\ \vdots \\ C_n \end{array} \right)
\]が成り立つことを示せます。（\( \vec{c} \) は任意定数を縦に並べた行列）

（導出）

\[ \vec{x} = e^{tA} \vec{c} \]が成り立つと仮定すると、\[\begin{align*}
\frac{d}{dt}  \vec{x} & = \frac{d}{dt} e^{tA} \vec{c}
\\ & = A e^{tA} \vec{c}
\\ & = A \vec{x}
\end{align*}\]となるので、\[
\frac{d}{dt}  \vec{x} = A \vec{x} \ \ \Rightarrow \ \ \vec{x} = e^{tA} \vec{c}
\]となることを示せます。

特に重要な法則3については導出を確認しておきましょう。

まず指数行列の定義式より、\[\begin{align*}
e^{PAP^{-1}} & = E + P^{-1}AP + \frac{1}{2!} (P^{-1}AP)^2 + \cdots + \frac{1}{n!} (P^{-1}AP)^n + \cdots
\\ & = \sum^{\infty}_{n = 0} \frac{1}{n!} (P^{-1}AP)^n
\end{align*}\]となりますね。

ここで、

となるので、\[
(P^{-1}AP)^n = P^{-1} A^n P
\]が成り立ちますね。

よって、\[\begin{align*}
e^{PAP^{-1}} & = P^{-1} \left( E + A + \frac{1}{2!} A^2 + \cdots +A^n + \cdots \right) P
\\ & = P^{-1} e^A P
\end{align*}\]と導出することができます。

(2) 主要な行列から指数行列への変換公式

まずは、主要な5つの行列に対しての指数行列の変形公式を確認しておきましょう。

この公式は指数行列を計算する上で重要になるので、必ず頭にいれておきましょう。

公式1～公式4については、下で導出しているので余裕がある人は確認してみてもいいかもしれません。

余裕ないぜっていう人は公式1だけでも頭にいれておくといいです。

指数行列の計算例1

行列\[
A = \left( \begin{array}{ccc} a & 0 \\ 0 & b \end{array} \right)
\]の指数行列 \( e^A \) が\[
e^A = \left( \begin{array}{ccc} e^a & 0 \\ 0 & e^b \end{array} \right) \]\[
e^{tA} = \left( \begin{array}{ccc} e^{at} & 0 \\ 0 & e^{bt} \end{array} \right)
\]になることを確認しましょう。

定義に沿って計算すると、\[\begin{align*}
e^A & = E + A + \frac{1}{2!} A^2 + \frac{1}{3!} A^3 +\cdots
\\ & = \left( \begin{array}{ccc} 1 & 0 \\ 0 & 1 \end{array} \right) +  \left( \begin{array}{ccc} a & 0 \\ 0 & b \end{array} \right) +  \frac{1}{2!} \left( \begin{array}{ccc} a & 0 \\ 0 & b \end{array} \right)^2 +  \frac{1}{3!} \left( \begin{array}{ccc} a & 0 \\ 0 & b \end{array} \right)^3 + \cdots
\\ & = \left( \begin{array}{ccc} 1 & 0 \\ 0 & 1 \end{array} \right) +  \left( \begin{array}{ccc} a & 0 \\ 0 & b \end{array} \right) +  \frac{1}{2!} \left( \begin{array}{ccc} a^2 & 0 \\ 0 & b^2 \end{array} \right) +  \frac{1}{3!} \left( \begin{array}{ccc} a^3 & 0 \\ 0 & b^3 \end{array} \right) + \cdots
\\ & = \left( \begin{array}{ccc} 1 + a + \frac{1}{2} a^2 + \frac{1}{3} a^3 + \cdots & 0 \\ 0 & 1 + b + \frac{1}{2} b^2 + \frac{1}{3} b^3 + \cdots \end{array} \right)
\\ & = \left( \begin{array}{ccc} e^a & 0 \\ 0 & e^b \end{array} \right)
\end{align*}\]と計算できます。

また、\[\begin{align*}
e^{tA} & = E + tA + \frac{1}{2!} (tA)^2 + \frac{1}{3!} (tA)^3 +\cdots
\\ & = \left( \begin{array}{ccc} 1 & 0 \\ 0 & 1 \end{array} \right) + t \left( \begin{array}{ccc} at & 0 \\ 0 & bt \end{array} \right) +  \frac{1}{2!} \left( \begin{array}{ccc} at & 0 \\ 0 & bt \end{array} \right)^2 + \frac{1}{3!} \left( \begin{array}{ccc} at & 0 \\ 0 & bt \end{array} \right)^3 + \cdots
\\ & = \left( \begin{array}{ccc} 1 & 0 \\ 0 & 1 \end{array} \right) + \left( \begin{array}{ccc} at & 0 \\ 0 & bt \end{array} \right) +  \frac{1}{2!} \left( \begin{array}{ccc} (at)^2 & 0 \\ 0 & (bt)^2 \end{array} \right) +  \frac{1}{3!} \left( \begin{array}{ccc} (at)^3 & 0 \\ 0 & (bt)^3 \end{array} \right) + \cdots
\\ & = \left( \begin{array}{ccc} 1 + at + \frac{1}{2} (at)^2 + \frac{1}{3} (at)^3 + \cdots & 0 \\ 0 & 1 + bt + \frac{1}{2} (bt)^2 + \frac{1}{3} (bt)^3 + \cdots \end{array} \right)
\\ & = \left( \begin{array}{ccc} e^{at} & 0 \\ 0 & e^{bt} \end{array} \right)
\end{align*}\]と計算できます。

指数行列の計算例2

行列\[
A = \left( \begin{array}{ccc} a & 1 \\ 0 & a \end{array} \right)
\]の指数行列 \( e^A \) が\[
e^A = \left( \begin{array}{ccc} e^a & e^a \\ 0 & e^a \end{array} \right) = e^a \left( \begin{array}{ccc} 1 & 1 \\ 0 & 1 \end{array} \right) \\
e^{tA} = \left( \begin{array}{ccc} e^{ta} & te^{ta} \\ 0 & e^{ta} \end{array} \right)
= e^{ta} \left( \begin{array}{ccc} 1 & t \\ 0 & 1 \end{array} \right)
\]になることを確認しましょう。

定義に沿って計算すると、\[\begin{align*}
e^A & = E + A + \frac{1}{2!} A^2 + \frac{1}{3!} A^3 +\cdots
\\ & = \left( \begin{array}{ccc} 1 & 0 \\ 0 & 1 \end{array} \right) +  \left( \begin{array}{ccc} a & 1 \\ 0 & a \end{array} \right) +  \frac{1}{2!} \left( \begin{array}{ccc} a & 1 \\ 0 & a \end{array} \right)^2 +  \frac{1}{3!} \left( \begin{array}{ccc} a & 1 \\ 0 & a \end{array} \right)^3 + \cdots
\\ & = \left( \begin{array}{ccc} 1 & 0 \\ 0 & 1 \end{array} \right) +  \left( \begin{array}{ccc} a & 1 \\ 0 & a \end{array} \right) +  \frac{1}{2!} \left( \begin{array}{ccc} a^2 & 2a \\ 0 & a^2 \end{array} \right) +  \frac{1}{3!} \left( \begin{array}{ccc} a^3 & 3a^2 \\ 0 & a^3 \end{array} \right) + \cdots
\\ & = \left( \begin{array}{ccc} 1 + a + \frac{1}{2} a^2 + \frac{1}{3} a^3 + \cdots & 1 + \frac{2}{2!} a + \frac{3}{3!} a^2 + \frac{4}{4!} a^3 \cdots \\ 0 & 1 + a + \frac{1}{2} a^2 + \frac{1}{3} a^3 + \cdots \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 + a + \frac{1}{2} a^2 + \frac{1}{3} a^3 + \cdots & 1 + a + \frac{1}{2!} a^2 + \frac{1}{3!} a^3 \cdots \\ 0 & 1 + a + \frac{1}{2} a^2 + \frac{1}{3} a^3 + \cdots \end{array} \right)
\\ & = \left( \begin{array}{ccc} e^a & e^a \\ 0 & e^a \end{array} \right)
\\ & = e^a \left( \begin{array}{ccc} 1 & 1 \\ 0 & 1 \end{array} \right)
\end{align*}\]と計算できます。

また、\[\begin{align*}
e^{tA} & = E + tA + \frac{1}{2!} (tA)^2 + \frac{1}{3!} (tA)^3 +\cdots
\\ & = \left( \begin{array}{ccc} 1 & 0 \\ 0 & 1 \end{array} \right) +  \left( \begin{array}{ccc} at & t \\ 0 & at \end{array} \right) +  \frac{1}{2!} \left( \begin{array}{ccc} at & t \\ 0 & at \end{array} \right)^2 +  \frac{1}{3!} \left( \begin{array}{ccc} at & t \\ 0 & at \end{array} \right)^3 + \cdots
\\ & = \left( \begin{array}{ccc} 1 & 0 \\ 0 & 1 \end{array} \right) +  \left( \begin{array}{ccc} at & t \\ 0 & t \end{array} \right) +  \frac{1}{2!} \left( \begin{array}{ccc} (at)^2 & 2at \\ 0 & (at)^2 \end{array} \right) +  \frac{1}{3!} \left( \begin{array}{ccc} (at)^3 & 3(at)^2 \\ 0 & (at)^3 \end{array} \right) + \cdots
\\ & = \left( \begin{array}{ccc} 1 + at + \frac{1}{2} (at)^2 + \frac{1}{3} (at)^3 + \cdots & t + \frac{2}{2!} at + \frac{3}{3!} (at)^2 + \frac{4}{4!} (at)^3 \cdots \\ 0 & 1 + at + \frac{1}{2} (at)^2 + \frac{1}{3} (at)^3 + \cdots \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 + at + \frac{1}{2} (at)^2 + \frac{1}{3} (at)^3 + \cdots & t \left( 1 + at + \frac{1}{2!} (at)^2 + \frac{1}{3!} (at)^3 \cdots \right) \\ 0 & 1 + at + \frac{1}{2} (at)^2 + \frac{1}{3} (at)^3 + \cdots \end{array} \right)
\\ & = \left( \begin{array}{ccc} e^{ta} & te^{ta} \\ 0 & e^{ta} \end{array} \right)
\\ & = e^{ta} \left( \begin{array}{ccc} 1 & t \\ 0 & 1 \end{array} \right)
\end{align*}\]と計算できます。

指数行列の計算例3

行列\[
A = \left( \begin{array}{ccc} 0 & -a \\ a & 0 \end{array} \right)
\]の指数行列 \( e^A \) が\[
e^A = \left( \begin{array}{ccc} \cos a & - \sin a \\ \sin a & \cos a \end{array} \right) \]\[
e^{tA} = \left( \begin{array}{ccc} \cos at & - \sin at \\ \sin at & \cos at \end{array} \right)
\]になることを確認しましょう。

定義に沿って計算すると、\[\begin{align*}
e^A & = E + A + \frac{1}{2!} A^2 + \frac{1}{3!} A^3 +\cdots
\\ & = \left( \begin{array}{ccc} 1 & 0 \\ 0 & 1 \end{array} \right) +  \left( \begin{array}{ccc} 0 & -a \\ a & 0 \end{array} \right) +  \frac{1}{2!} \left( \begin{array}{ccc} 0 & -a \\ a & 0 \end{array} \right)^2 +  \frac{1}{3!} \left( \begin{array}{ccc} 0 & -a \\ a & 0 \end{array} \right)^3 + \cdots
\\ & = \left( \begin{array}{ccc} 1 & 0 \\ 0 & 1 \end{array} \right) +  \left( \begin{array}{ccc} 0 & -a \\ a & 0 \end{array} \right) +  \frac{1}{2!} \left( \begin{array}{ccc} -a^2 & 0 \\ 0 & -a^2 \end{array} \right) +  \frac{1}{3!} \left( \begin{array}{ccc} 0 & a^3 \\ -a^3 & 0 \end{array} \right) + \cdots
\\ & = \left( \begin{array}{ccc} 1 - \frac{1}{2!} a^2 + \frac{1}{4!} a^4 + \cdots & - \left( a- \frac{1}{3} a^3 + \frac{1}{5} a^5 + \cdots \right) \\ a- \frac{1}{3} a^3 + \frac{1}{5} a^5 + \cdots &  1 - \frac{1}{2!} a^2 + \frac{1}{4!} a^4 + \cdots \end{array} \right)
\\ & = \left( \begin{array}{ccc} \cos a & - \sin a \\ \sin a & \cos a \end{array} \right)
\end{align*}\]と計算できます。

また、\[\begin{align*}
e^{tA} & = E + tA + \frac{1}{2!} (tA)^2 + \frac{1}{3!} (tA)^3 +\cdots
\\ & = \left( \begin{array}{ccc} 1 & 0 \\ 0 & 1 \end{array} \right) +  \left( \begin{array}{ccc} 0 & -at \\ at & 0 \end{array} \right) +  \frac{1}{2!} \left( \begin{array}{ccc} 0 & -at \\ at & 0 \end{array} \right)^2 +  \frac{1}{3!} \left( \begin{array}{ccc} 0 & -at \\ at & 0 \end{array} \right)^3 + \cdots
\\ & = \left( \begin{array}{ccc} 1 & 0 \\ 0 & 1 \end{array} \right) +  \left( \begin{array}{ccc} 0 & -at \\ at & 0 \end{array} \right) +  \frac{1}{2!} \left( \begin{array}{ccc} -(at)^2 & 0 \\ 0 & -(at)^2 \end{array} \right) +  \frac{1}{3!} \left( \begin{array}{ccc} 0 & (at)^3 \\ -(at)^3 & 0 \end{array} \right) + \cdots
\\ & = \left( \begin{array}{ccc} 1 - \frac{1}{2!} (at)^2 + \frac{1}{4!} (at)^4 + \cdots & - \left( at - \frac{1}{3} (at)^3 + \frac{1}{5} (at)^5 + \cdots \right) \\ t - \frac{1}{3} (at)^3 + \frac{1}{5} (at)^5 + \cdots &  1 - \frac{1}{2!} (at)^2 + \frac{1}{4!} (at)^4 + \cdots \end{array} \right)
\\ & = \left( \begin{array}{ccc} \cos at & - \sin at \\ \sin at & \cos at \end{array} \right)
\end{align*}\]と計算できます。

行列版オイラーの公式？

行列\[
A = \left( \begin{array}{ccc} 0 & -a \\ a & 0 \end{array} \right) = a \left( \begin{array}{ccc} 0 & -1 \\ 1 & 0 \end{array} \right)
\]に対し、\[\begin{align*}
e^A & = \left( \begin{array}{ccc} \cos a & - \sin a \\ \sin a & \cos a \end{array} \right)
\\ & = \cos a \left( \begin{array}{ccc} 1 & 0 \\ 0 & 1 \end{array} \right) + \sin a \left( \begin{array}{ccc} 0 & -1 \\ 1 & 0 \end{array} \right)
\end{align*}\]となることを確認しました。

ここで、\[
K = \left( \begin{array}{ccc} 0 & -1 \\ 1 & 0 \end{array} \right) \]\[
e^A = E \cos a + J \sin a
\]のようなオイラーの公式っぽいものが出てきます。

さらに面白いことに\[
J^2 = \left( \begin{array}{ccc} -1 & 0 \\ 0 & -1 \end{array} \right) = -E
\]となり、まるで虚数の定義（\( i^2 = -1 \)）にそっくりな式 \( J^2 = -E \) が導出できちゃうのです！

指数行列の計算例4

行列\[
A = \left( \begin{array}{ccc} a & -b \\ b & a \end{array} \right)
\]の指数行列 \( e^A \) が\[
e^A = e^{a} \left( \begin{array}{ccc} \cos b & - \sin b \\ \sin b & \cos b \end{array} \right) \]\[
e^{tA} = e^{at} \left( \begin{array}{ccc} \cos bt & - \sin bt \\ \sin bt & \cos bt \end{array} \right)
\]になることを確認しましょう。

行列 \( B \), \( C \) を\[
B = \left( \begin{array}{ccc} a & 0 \\ 0 & a \end{array} \right) \]\[
C = \left( \begin{array}{ccc} 0 & -b \\ b & 0 \end{array} \right)
\]とすると、\[ A = B + C \]\[
e^B = \left( \begin{array}{ccc} e^a & 0 \\ 0 & e^a \end{array} \right) \]\[
e^C = \left( \begin{array}{ccc} \cos b & - \sin b \\ \sin b & \cos b \end{array} \right)
\]となる。

また、\[
BC = CB = \left( \begin{array}{ccc} 0 & -ab \\ ab & 0 \end{array} \right)
\]となるので、 \[
e^A = e^{B+C} = e^B e^C
\]が成立する。

（指数関数の定理1：\( BC = CB \) の確認を忘れずに！）

よって、\[\begin{align*}
e^A & = e^B e^C
\\ & = \left( \begin{array}{ccc} e^a & 0 \\ 0 & e^a \end{array} \right) \left( \begin{array}{ccc} \cos b & - \sin b \\ \sin b & \cos b \end{array} \right)
\\ & = e^a \left( \begin{array}{ccc} \cos b & - \sin b \\ \sin b & \cos b \end{array} \right)
\end{align*} \]と変形できる。

また、\[
e^{tB} = \left( \begin{array}{ccc} e^{at} & 0 \\ 0 & e^{at} \end{array} \right) \]\[
e^{tC} = \left( \begin{array}{ccc} \cos bt & - \sin bt \\ \sin bt & \cos bt \end{array} \right)
\]となり、\( BC = CB \) なので、\[\begin{align*}
e^{tA} & = e^{tB} e^{tC}
\\ & = \left( \begin{array}{ccc} e^{at} & 0 \\ 0 & e^{at} \end{array} \right) \left( \begin{array}{ccc} \cos bt & - \sin bt \\ \sin bt & \cos bt \end{array} \right)
\\ & = e^{at} \left( \begin{array}{ccc} \cos bt & - \sin bt \\ \sin bt & \cos bt \end{array} \right)
\end{align*} \]と変形できる。

(3) 主要な公式以外の導出

先程は、定義式\[\begin{align*}
e^A & = E + A + \frac{1}{2!} A^2 + \cdots + \frac{1}{n!} A^n + \cdots
\\ & = \sum^{\infty}_{n = 0} \frac{1}{n!} A^n
\end{align*}\]もしくは\[\begin{align*}
e^{tA} & = E + tA + \frac{1}{2!} (tA)^2 + \cdots + \frac{1}{n!} (tA)^n + \cdots
\\ & = \sum^{\infty}_{n = 0} \frac{1}{n!} (tA)^n
\end{align*}\]から変形をすることで、指数行列を計算しました。

しかし、いちいち定義式を変形して計算するのは結構めんどくさいです。

そこで、行列の対角化などにより \( A = P^{-1} D P \) を算出し、\[
e^A = e^{PDP^{-1}} = P e^{D} P^{-1} \]\[
e^{tA} = e^{t PDP^{-1}} = P e^{tD} P^{-1}
\]を計算することで、定義式を変形することなく指数行列を求めることができます。

（ただし \( D \) を主要な行列の形に変える）

例題で1つ試してみましょう。

例題2

行列\[
A = \left( \begin{array}{ccc} 1 & 2 \\ 2 & 1 \end{array} \right)
\]の指数行列 \( e^{tA} \) を求めなさい。

解説2

例題1より、行列 \( A \) は\[
P = \left( \begin{array}{ccc} 1 & 1 \\ -1 & 1 \end{array} \right)
\]を用いて\[
P^{-1} A P = \left( \begin{array}{ccc} -1 & 0 \\ 0 & 3 \end{array} \right) = D
\]と対角化できます。

また、（公式1）より \( e^{tD} \) は\[
e^{tD} = \left( \begin{array}{ccc} e^{-t} & 0 \\ 0 & e^{3t} \end{array} \right)
\]と導出できます。

さらに、\( P \) の逆行列 \( P^{-1} \) は\[
P^{-1} = \frac{1}{2} \left( \begin{array}{ccc} 1 & -1 \\ 1 & 1 \end{array} \right)
\]となります。（例題1の(3)で計算済）

よって、\[\begin{align*}
e^{tA} & = P e^{tD} P^{-1}
\\ & = \left( \begin{array}{ccc} 1 & 1 \\ -1 & 1 \end{array} \right)  \left( \begin{array}{ccc} e^{-t} & 0 \\ 0 & e^{3t} \end{array} \right) \cdot \frac{1}{2} \left( \begin{array}{ccc} 1 & -1 \\ 1 & 1 \end{array} \right)
\\ & = \frac{1}{2} \left( \begin{array}{ccc} e^{-t} & e^{3t} \\ -e^{-t} & e^{3t} \end{array} \right) \left( \begin{array}{ccc} 1 & -1 \\ 1 & 1 \end{array} \right)
\\ & = \frac{1}{2} \left( \begin{array}{ccc} e^{-t} + e^{3t} & -e^{-t} + e^{3t} \\ -e^{-t} + e^{3t} & e^{-t} + e^{3t} \end{array} \right)
\end{align*}\]と計算できる。

例題3～例題5でも、指数行列 \( e^{tA} \) を求める問題を用意しているので計算練習をしたい人はご覧ください。

４．指数行列を用いた連立微分方程式の解き方

指数行列を用いることで連立微分方程式\[
\frac{d}{dt}  \vec{x} = A \vec{x}
\]を\[
\vec{x} = e^{tA} \vec{c} , \ \ \ \vec{c} = \left( \begin{array}{ccc} C_1 \\ C_2 \\ \vdots \\ C_n \end{array} \right)
\]と変形できるので、\( e^{tA} \) を求めることで簡単に連立微分方程式の解が求まります。

（初期値が与えられている場合は、\( \vec{c} \) に初期値\[
\vec{c} = \left( \begin{array}{ccc} x_1 (0) \\ x_2 (0) \\ \vdots \\ x_n (0) \end{array} \right)
\]を入れることで初期条件を考慮した解を求めることができます。）

(1) 係数行列が対角化可能かつ固有値がすべて実数の場合

まずは、係数行列 \( A \) が対角化可能な場合を見ていきましょう。

なお、対角化可能の場合は、例題1のように解くことで指数行列 \( e^{tA} \) の形にしなくても解くことができます。

例題3

連立微分方程式\[
\left\{ \begin{array}{l} \frac{dx}{dt} = 4x + y \\ \frac{dy}{dt} = -8x - 5y \end{array}\right.
\]は、行列を用いて\[
\frac{d}{dt} \left( \begin{array}{ccc} x \\ y \end{array} \right) = \left( \begin{array}{ccc} 4 & 1 \\ -8 & -5 \end{array} \right) \left( \begin{array}{ccc} x \\ y \end{array} \right) \]\[
\frac{d \vec{x} }{dt} = A \vec{x}
\]と表される。これについて、(1)～(3)の問いに答えなさい。

(1) 行列\[
A = \left( \begin{array}{ccc} 4 & 1 \\ -8 & -5 \end{array} \right)
\]の固有値、固有ベクトルを求め、対角化しなさい。

(2) (1)を用いて連立微分方程式の一般解を求めなさい。

(3) 行列 \( A \) の指数行列 \( e^{tA} \) を求めなさい。

解説3

(1)

固有値を \( k \) とすると、\[\begin{align*}
|A - kE| & = \left| \begin{array}{ccc} 4-k & 1 \\ -8 & -5-k \end{array} \right|
\\ & = (k-4)(k+5) + 8
\\ & = k^2 + k - 20 + 8
\\ & =k^2 + k - 12
\\ & = (k-3)(k+4)
\\ & = 0
\end{align*}\]と変形できるので、固有値は 3, -4 となる。

（検算：固有値の総和 = 対角成分の総和 = -1）

つぎに、対応する固有値ごとに固有ベクトルを求める。

(i) 固有値が3のときの固有ベクトル \( \vec{p}_1 \)

行列 \( A - 3E \) の変形を行うと、\[\begin{align*}
A - 3E & = \left( \begin{array}{ccc} 1 & 1 \\ -8 & -8 \end{array} \right) \\ & \to \left( \begin{array}{ccc} 1 & 1 \\ 0 & 0 \end{array} \right)
\end{align*}\]となる。方程式\[
x + y = 0
\]の解は任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ -1 \end{array} \right)
\]となるので、固有ベクトル \( \vec{p}_1 \) は\[
\vec{p}_1 = \left( \begin{array}{ccc} 1 \\ -1 \end{array} \right)
\]となる。

(ii) 固有値が-4のときの固有ベクトル \( \vec{p}_2 \)

行列 \( A + 4E \) の変形を行うと、\[\begin{align*}
A + 4E & = \left( \begin{array}{ccc} 8 & 1 \\ -8 & -1 \end{array} \right) \\ & \to \left( \begin{array}{ccc} 8 & 1 \\ 0 & 0 \end{array} \right)
\end{align*}\]となる。方程式\[
8x + y = 0
\]の解は任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ -8 \end{array} \right)
\]となるので、固有ベクトル \( \vec{p}_2 \) は\[
\vec{p}_2 = \left( \begin{array}{ccc} 1 \\ -8 \end{array} \right)
\]となる。

よって、行列 \( P \) を\[
P = \left( \begin{array}{ccc} \vec{p}_1 \\ \vec{p}_2 \end{array} \right) = \left( \begin{array}{ccc} 1 & 1 \\ -1 & -8 \end{array} \right)
\]とすることで、\[
P^{-1} A P = \left( \begin{array}{ccc} 3 & 0 \\ 0 & -4 \end{array} \right) = D
\]と対角化することができます。

[検算]\[
AP = PD = \left( \begin{array}{ccc} 3 & -4 \\ -3 & 32 \end{array} \right)
\]

(2)

連立方程式\[
\frac{d \vec{x} }{dt} = A \vec{x}
\]の一般解は、任意定数を縦に並べたベクトル \( \vec{c} \) を用いて\[
\vec{x} = e^{tA} \vec{c}
\]で求めることができる。

また、対角化の式\[
P^{-1} AP = D
\]に左辺から \( P \)、右辺から \( P^{-1} \) を掛けると\[\begin{align*}
\color{red}{P} P^{-1} AP \color{blue}{P^{-1}} & = \color{red}{P} D \color{blue}{P^{-1}} \\
A & = P D P^{-1}
\end{align*}\]が成立することがわかるので、\[\begin{align*}
\vec{x} & = e^{tA} \vec{c} \\ & = e^{t P DP^{-1}} \vec{c}
\\ & = P e^{tD} P^{-1} \vec{c}
\end{align*}\]が成立する。（法則3の変形）

また、公式1より\[
e^{tD} = \left( \begin{array}{ccc} e^{3t} & 0 \\ 0 & e^{-4t} \end{array} \right)
\]となる。

ここで、改めて任意定数を\[
\vec{c'} = P^{-1} \vec{c} = \left( \begin{array}{ccc} C_1 \\ C_2 \end{array} \right)
\]とすることで、\[\begin{align*}
\vec{x} & = P e^{tD} P^{-1} \vec{c}
\\ & = P e^{tD} \vec{c'}
\\ & = \left( \begin{array}{ccc} 1 & 1 \\ -1 & -8 \end{array} \right) \left( \begin{array}{ccc}  e^{3t} & 0 \\ 0 & e^{-4t} \end{array} \right) \left( \begin{array}{ccc} C_1 \\ C_2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} e^{3t} & e^{-4t} \\ - e^{3t} & -8 e^{-4t} \end{array} \right)  \left( \begin{array}{ccc} C_1 \\ C_2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} C_1 e^{3t} + C_2 e^{4t} \\ - C_1 e^{3t} - 8 C_2 e^{-4t} \end{array} \right)
\end{align*} \]となるので、一般解を\[
\left\{ \begin{array}{l} x = C_1 e^{3t} + C_2 e^{4t} \\ y = - C_1 e^{3t} - 8 C_2 e^{-4t} \end{array}\right.
\]と求めることができる。

(3)

\( P \) の逆行列 \( P^{-1} \) は\[
P^{-1} = \frac{1}{7} \left( \begin{array}{ccc} 8 & 1 \\ -1 & -1 \end{array} \right)
\]となる。

よって、\[\begin{align*}
e^{tA} & = P e^{tD} P^{-1}
\\ & = \left( \begin{array}{ccc} 1 & 1 \\ -1 & 1 \end{array} \right)  \left( \begin{array}{ccc} e^{-t} & 0 \\ 0 & e^{3t} \end{array} \right) \cdot \frac{1}{7} \left( \begin{array}{ccc} 8 & 1 \\ -1 & -1 \end{array} \right)
\\ & = \frac{1}{7} \left( \begin{array}{ccc} e^{3t} & e^{-4t} \\ - e^{3t} & -8 e^{-4t} \end{array} \right) \left( \begin{array}{ccc} 8 & 1 \\ -1 & -1 \end{array} \right)
\\ & = \frac{1}{7} \left( \begin{array}{ccc} 8 e^{3t} - e^{-4t} & e^{3t} - e^{-4t} \\ - 8 e^{3t} + 8 e^{-4t} & - e^{3t} + 8 e^{-4t}  \end{array} \right)
\end{align*}\]と計算できる。

(2) 係数行列が対角化できない場合

残念ながら、すべての行列が対角化できるとは限りません。

ですが、正則な行列 \( P \) を用いて、できる限り対角行列の近い形\[
P^{-1} AP = J = \left( \begin{array}{ccc} a & 1 \\ 0 & a \end{array} \right)
\]つまりジョルダン標準形に変形することはできますね。

そこで、対角化ができない場合はジョルダン標準形を求め、\( A = PJP^{-1} \) の形にすることで指数行列を用いて連立微分方程式の一般解を求めることができます。

（ジョルダン標準形ってなんだっけ？もしくは忘れてしまったという人は下の記事で復習することをおすすめします。）

www.momoyama-usagi.com

例題4

連立微分方程式\[
\left\{ \begin{array}{l} \frac{dx}{dt} = 2x + y \\ \frac{dy}{dt} = -4x + 6y \end{array}\right.
\]は、行列を用いて\[
\frac{d}{dt} \left( \begin{array}{ccc} x \\ y \end{array} \right) = \left( \begin{array}{ccc} 2 & 1 \\ -4 & 6 \end{array} \right) \left( \begin{array}{ccc} x \\ y \end{array} \right) \]\[
\frac{d \vec{x} }{dt} = A \vec{x}
\]と表される。これについて、(1)～(3)の問いに答えなさい。

(1) 行列\[
A = \left( \begin{array}{ccc} 2 & 1 \\ -4 & 6 \end{array} \right)
\]を正則行列 \( P \) を用いて、\( P^{-1} AP \) をジョルダン標準形にしなさい。

(2) (1)を用いて連立微分方程式の一般解を求めなさい。

(3) 行列 \( A \) の指数行列 \( e^{tA} \) を求めなさい。

解説4

(1)

固有値を \( k \) とすると、\[\begin{align*}
|A - kE| & = \left| \begin{array}{ccc} 2-t & 1 \\ -4 & 6-t \end{array} \right|
\\ & = (k-2)(k-6) + 4
\\ & = k^2  - kt + 12 + 4
\\ & = k^2  - 8k + 16
\\ & = (k-4)^2
\\ & = 0
\end{align*}\]と変形できるので、固有値は4（2重解）となる。

（検算：固有値の総和 = 対角成分の総和 = 4）

つぎに、対応する固有値ごとに固有ベクトルを求める。

(i) 固有値が4のときの固有ベクトル \( \vec{p}_1 \)

行列 \( A - 3E \) の変形を行うと、\[\begin{align*}
A - 4E & = \left( \begin{array}{ccc} -2 & 1 \\ -4 & 2 \end{array} \right) \\ & \to \left( \begin{array}{ccc} 1 & 1 \\ 0 & 0 \end{array} \right)
\end{align*}\]となる。方程式\[
2x - y = 0
\]の解は任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 2 \end{array} \right)
\]となるので、固有ベクトル \( \vec{p}_1 \) は\[
\vec{p}_1 = \left( \begin{array}{ccc} 1 \\ 2 \end{array} \right)
\]となる。

固有ベクトルが1本ないので対角化ができない。

そこで、\[
(A-4E) \vec{p}_2 = \vec{p}_1
\]を満たすような行列を考える。\[\begin{align*}
A - 4E & = \left( \begin{array}{cc|c} -2 & 1 & 1 \\ -4 & 2 & 2 \end{array} \right) \\  & \to \left( \begin{array}{cc|c} 2 & -1 & -1 \\ 0 & 0 & 0 \end{array} \right)
\end{align*}\]となる。方程式\[
2x - y = -1
\]の解の1つに\[
\left( \begin{array}{ccc} x \\ y \end{array} \right) = \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right)
\]があるので、ベクトル \( \vec{p}_2 \) は\[
\vec{p}_2 = \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right)
\]と求まる。

よって、\[
\left\{ \begin{array}{l} (A - 4E) \vec{p_1} = \vec{0} \\ A \vec{p_1} = 4 \vec{p_1} \end{array}\right.  \ \ \
\left\{ \begin{array}{l} (A - 4E) \vec{p_2} = \vec{p_1} \\ A \vec{p_2} = \vec{p_1} + 4 \vec{p_2} \end{array}\right.
\]が成立するので、\[ P = \left( \vec{p_1}, \vec{p_2} \right) = \left( \begin{array}{ccc} 1 & 0 \\ 2 & 1 \end{array} \right)\]とすると、\[ \begin{align*}
AP & = A \left( \vec{p_1}, \vec{p_2} \right) \\ & = \left( 4 \vec{p_1}, \vec{p_1} + 4 \vec{p_2} \right)  \\ & =   \left( \vec{p_1}, \vec{p_2} \right) \left( \begin{array}{ccc} 4 & 1 \\ 0 & 4 \end{array} \right) \\ & = P \left( \begin{array}{ccc} 4 & 1 \\ 0 & 4 \end{array} \right)
\end{align*} \]となるので、\[
P^{-1} A P = \left( \begin{array}{ccc} 4 & 1 \\ 0 & 4 \end{array} \right) = J
\]とジョルダン標準形にすることができます。

[検算]\[
AP = PJ = \left( \begin{array}{ccc} 4 & 1 \\ 8 & 6 \end{array} \right)
\]

(2)

連立方程式\[
\frac{d \vec{x} }{dt} = A \vec{x}
\]の一般解は、任意定数を縦に並べたベクトル \( \vec{c} \) を用いて\[
\vec{x} = e^{tA} \vec{c}
\]で求めることができる。

また、ジョルダン標準形の式\[
P^{-1} AP = J
\]に左辺から \( P \)、右辺から \( P^{-1} \) を掛けると\[\begin{align*}
\color{red}{P} P^{-1} AP \color{blue}{P^{-1}} & = \color{red}{P} D \color{blue}{P^{-1}} \\
A & = P J P^{-1}
\end{align*}\]が成立することがわかるので、\[\begin{align*}
\vec{x} & = e^{tA} \vec{c} \\ & = e^{t P JP^{-1}} \vec{c}
\\ & = P e^{tJ} P^{-1} \vec{c}
\end{align*}\]が成立する。（法則3の変形）

また、公式1より\[
e^{tJ} = e^{4t} \left( \begin{array}{ccc} 1 & t \\ 0 & 1 \end{array} \right)
\]となる。

ここで、改めて任意定数を\[
\vec{c'} = P^{-1} \vec{c} = \left( \begin{array}{ccc} C_1 \\ C_2 \end{array} \right)
\]とすることで、\[\begin{align*}
\vec{x} & = P e^{tD} P^{-1} \vec{c}
\\ & = P e^{tD} \vec{c'}
\\ & = \left( \begin{array}{ccc} 1 & 0 \\ 2 & 1 \end{array} \right) \cdot e^{4t} \left( \begin{array}{ccc} 1 & t \\ 0 & 1 \end{array} \right) \left( \begin{array}{ccc} C_1 \\ C_2 \end{array} \right)
\\ & = e^{4t} \left( \begin{array}{ccc} 1 & t \\ 2 & 2t+1 \end{array} \right)  \left( \begin{array}{ccc} C_1 \\ C_2 \end{array} \right)
\\ & = e^{4t} \left( \begin{array}{ccc} C_1 + C_2 t  \\ 2 C_1 + (2t+1) C_2 \end{array} \right)
\end{align*} \]となるので、一般解を\[
\left\{ \begin{array}{l} x = C_1 e^{4t} + C_2 t e^{4t} \\ y = 2 C_1 e^{4t} + C_2 e^{4t} (2t+1)　\end{array}\right.
\]と求めることができる。

(3)

\( P \) の逆行列 \( P^{-1} \) は\[
P^{-1} =  \left( \begin{array}{ccc} 1 & 0 \\ -2 & 1 \end{array} \right)
\]となる。

よって、\[\begin{align*}
e^{tA} & = P e^{tD} P^{-1}
\\ & = \left( \begin{array}{ccc} 1 & 0 \\ 2 & 1 \end{array} \right) \cdot e^{4t} \left( \begin{array}{ccc} 1 & t \\ 0 & 1 \end{array} \right) \left( \begin{array}{ccc} 1 & 0 \\ -2 & 1 \end{array} \right)
\\ & = e^{4t} \left( \begin{array}{ccc} 1 & t \\ 2 & 2t+1 \end{array} \right) \left( \begin{array}{ccc} 1 & 0 \\ 2 & 1 \end{array} \right)
\\ & = e^{4t} \left( \begin{array}{ccc} -2t+1 & t \\ -4t & 2t+1 \end{array} \right)
\end{align*}\]と計算できる。

(3) 固有値が共役な複素数になる場合

※ 複素数計算に慣れていない人は、こちらの記事で練習をおすすめします。

行列 \( A \) の固有値が共役な複素数 \( a \pm b i \) となる場合も、(1)と同じように対角化を用いることで連立微分方程式を解いたり、\( e^{tA} \) を求めることができます。

しかし、ここでは対角化ができる場合でもあえて対角化を行わないことを考えます。

ある固有値 \( a + bi \) の固有ベクトルが \( \vec{p} \) で表せるとします。

すると、数式\[
A \vec{p} = (a+bi) \vec{p}
\]が成立しますね。（固有ベクトルの定義）

ここで、固有ベクトル \( \vec{p} \) を\[
\vec{p} = \vec{u} + i \vec{v}
\]とすることで実部 \( \vec{u} \) と虚部 \( \vec{v} \) に分離します。

すると、左辺は\[\begin{align*}
A \vec{p}  & = A ( \vec{u} + i \vec{v} )
\\ & = A \vec{u} + i A \vec{v}
\end{align*}\]と分離でき、右辺は\[\begin{align*}
(a+bi) \vec{p} & = (a+bi) ( \vec{u} + i \vec{v} )
\\ & = a \vec{u} + ai \vec{v} + bi \vec{u} - b \vec{v}
\\ & = ( a \vec{u} - b \vec{v} ) + i (a \vec{v} + b \vec{u} )
\end{align*}\]となるので、\[
A \vec{p} = (a+bi) \vec{p} \]\[
A \vec{u} + i A \vec{v} =  ( a \vec{u} - b \vec{v} ) + i (a \vec{v} + b \vec{u} )
\]が成り立ちます。

よって、\[
\left\{ \begin{array}{l} A \vec{u} = a \vec{u} - b \vec{v} \\ A \vec{v} = b \vec{u} + a \vec{v}  \end{array}\right.
\]の形に変形できるので、行列を用いて\[
A \left( \begin{array}{ccc} \vec{u}  & \vec{v} \end{array} \right)  = \left( \begin{array}{ccc} \vec{u}  & \vec{v} \end{array} \right) \left( \begin{array}{ccc} a & b \\ -b & a \end{array} \right)
\]と表すことができます。

ここで、\[
P = \left( \begin{array}{ccc} \vec{u}  & \vec{v} \end{array} \right), \ \ \ X =  \left( \begin{array}{ccc} a & b \\ - b & a \end{array} \right)
\]とおくことで\[
AP = PX \]\[
A P \color{red}{P^{-1}} = P X \color{red}{P^{-1}} \]\[
A = P X P^{-1}
\]の形に変形することができます。

ここで、\[
e^{tX} = e^{at} \left( \begin{array}{ccc} \cos bt & - \sin bt \\ \sin bt & \cos bt \end{array} \right)
\]と計算できるので、\[\begin{align*}
e^{A} & = e^{tP X P^{-1}} \\ & = P e^{tX} P^{-1}
\end{align*}\]とすることで、対角化をすることなく指数行列 \( e^{tA} \) を求めることができますね。

というわけで、例題で確認してみましょう。

例題5

連立微分方程式\[
\left\{ \begin{array}{l} \frac{dx}{dt} = -x - 5y \\ \frac{dy}{dt} = x + 3y \end{array}\right.
\]は、行列を用いて\[
\frac{d}{dt} \left( \begin{array}{ccc} x \\ y \end{array} \right) = \left( \begin{array}{ccc} -1 & -5 \\ 1 & 3 \end{array} \right) \left( \begin{array}{ccc} x \\ y \end{array} \right) \]\[
\frac{d \vec{x} }{dt} = A \vec{x}
\]と表される。これについて、(1)～(3)の問いに答えなさい。

(1) 行列\[
A = \left( \begin{array}{ccc} -1 & -5 \\ 1 & 3 \end{array} \right)
\]の固有値、固有ベクトルを求めなさい。

(2) (1)を用いて連立微分方程式の一般解を求めなさい。

(3) 行列 \( A \) の指数行列 \( e^{tA} \) を求めなさい。

解説5

(1)

固有値を \( t \) とすると、\[\begin{align*}
|A - tE| & = \left| \begin{array}{ccc} -1-t & -5 \\ 1 & 3-t \end{array} \right|
\\ & = (t+1)(t-3) + 5
\\ & = t^2 - 2t + 2
\\ & = 0
\end{align*}\]となる。ここで、\[
\frac{1 \pm \sqrt{4-8}}{2} = 1 \pm i
\]変形できるので、固有値は 1+i, 1-i となる。

（検算：固有値の総和 = 対角成分の総和 = 2）

つぎに、対応する固有値ごとに固有ベクトルを求める。

ここで、計算のコツなのですが、固有値が複素数のときはすぐ行基本変形をせず、\[
A \vec{p} = t \vec{p} \]\[
A \left( \begin{array}{ccc} x \\ y \end{array} \right) = t \left( \begin{array}{ccc} x \\ y \end{array} \right)
\]の連立方程式を一旦組み立ててから解くのがおすすめです。

(i) 固有値が 1+i のときの固有ベクトル \( \vec{p}_1 \)

固有値が \( 1 + i \) のとき、\[
\left\{ \begin{array}{l} -x - 5y = (1+i) x \\ x + 3y = (1+i) 3y \end{array}\right.
\]となるので、1式目を変形して\[
(2+i) x = -5y \]\[
y = - \frac{1}{5} (2+i)
\]とする。ここで、\( x = 2 - i \) とすると、\[
y = - \frac{1}{5} (2+i)(2-i) = -1
\]となるので、解の1つが\[
y = \left( \begin{array}{ccc} 2-i \\ -1 \end{array} \right)
\]となる。

よって固有ベクトル \( \vec{p}_1 \) は\[
\vec{p}_1 = \left( \begin{array}{ccc} 2-i \\ -1 \end{array} \right)
\]と求まる。

(ii) 固有値が1-iのときの固有ベクトル \( \vec{p}_2 \)

固有値が \( 1 - i \) のとき、\[
\left\{ \begin{array}{l} -x - 5y = (1-i) x \\ x + 3y = (1-i) 3y \end{array}\right.
\]となるので、1式目を変形して\[
(2-i) x = -5y \]\[
y = - \frac{1}{5} (2-i)
\]とする。ここで、\( x = 2 + i \) とすると、\[
y = - \frac{1}{5} (2-i)(2+i) = -1
\]となるので、解の1つが\[
y = \left( \begin{array}{ccc} 2+i \\ -1 \end{array} \right)
\]となる。

よって固有ベクトル \( \vec{p}_2 \) は\[
\vec{p}_2 = \left( \begin{array}{ccc} 2+i \\ -1 \end{array} \right)
\]と求まる。

(2)

ここで、固有値 \( t = 1+i \) に対する固有ベクトル\[
\vec{p} = \left( \begin{array}{ccc} 2-i \\ -1 \end{array} \right)
\]を考える。

ここで、固有ベクトル \( \vec{p} \) を\[\begin{align*}
\vec{p} & = \vec{u} + i \vec{v}
\\ & =  \left( \begin{array}{ccc} 2 \\ -1 \end{array} \right) + i  \left( \begin{array}{ccc} -1 \\ 0 \end{array} \right)
\end{align*} \]とする。

すると、左辺は\[\begin{align*}
A \vec{p}  & = A ( \vec{u} + i \vec{v} )
\\ & = A \vec{u} + i A \vec{v}
\end{align*}\]と分離でき、右辺は\[\begin{align*}
(1+i) \vec{p} & = (1+i) ( \vec{u} + i \vec{v} )
\\ & =  \vec{u} + i \vec{v} + i \vec{u} -  \vec{v}
\\ & = (  \vec{u} -  \vec{v} ) + i ( \vec{v} +  \vec{u} )
\end{align*}\]となるので、\[
A \vec{p} = (1+i) \vec{p} \]\[
A \vec{u} + i A \vec{v} =  ( \vec{u} -  \vec{v} ) + i ( \vec{v} +  \vec{u} )
\]が成り立ちます。

よって、\[
\left\{ \begin{array}{l} A \vec{u} =  \vec{u} - \vec{v} \\ A \vec{v} = \vec{u} + \vec{v}  \end{array}\right.
\]の形に変形できるので、行列を用いて\[
A \left( \begin{array}{ccc} \vec{u}  & \vec{v} \end{array} \right)  = \left( \begin{array}{ccc} \vec{u}  & \vec{v} \end{array} \right) \left( \begin{array}{ccc} 1 & 1 \\ -1 & 1 \end{array} \right)
\]と表すことができます。

ここで、\[
P = \left( \begin{array}{ccc} \vec{u}  & \vec{v} \end{array} \right) = \left( \begin{array}{ccc} 2 & -1 \\ -1 & 0 \end{array} \right)　\\ X =  \left( \begin{array}{ccc} 1 & 1 \\ -1 & 1 \end{array} \right)
\]とおくことで\[
AP = PX \]\[
A P \color{red}{P^{-1}} = P X \color{red}{P^{-1}} \]\[
A = P X P^{-1}
\]の形に変形することができます。

[検算]\[
AP = PX = \left( \begin{array}{ccc} 3 & 1 \\ -1 & -1 \end{array} \right)
\]

ここで、連立方程式\[
\frac{d \vec{x} }{dt} = A \vec{x}
\]の一般解は、任意定数を縦に並べたベクトル \( \vec{c} \) を用いて\[
\vec{x} = e^{tA} \vec{c}
\]で求めることができる。

また、\[
A = P X P^{-1}
\]なので、\[\begin{align*}
\vec{x} & = e^{tA} \vec{c} \\ & = e^{t P X P^{-1} } \vec{c}
\\ & = P e^{tX} P^{-1} \vec{c}
\end{align*}\]が成立する。（法則3の変形）

また、公式1より\[
e^{tX} = e^{t} \left( \begin{array}{ccc} \cos t & \sin t \\ - \sin t & \cos t \end{array} \right)
\]となる。

ここで、改めて任意定数を\[
\vec{c'} = P^{-1} \vec{c} = \left( \begin{array}{ccc} C_1 \\ C_2 \end{array} \right)
\]とすることで、\[\begin{align*}
\vec{x} & = P e^{tX} P^{-1} \vec{c}
\\ & = P e^{tX} \vec{c'}
\\ & = \left( \begin{array}{ccc} 2 & -1 \\ -1 & 0 \end{array} \right) \cdot e^{t} \left( \begin{array}{ccc} \cos t & \sin t \\ - \sin t & \cos t \end{array} \right) \left( \begin{array}{ccc} C_1 \\ C_2 \end{array} \right)
\\ & = e^{t} \left( \begin{array}{ccc} 2 \cos t + \sin t & 2 \sin t - \cos t \\ - \cos t & - \sin t \end{array} \right)  \left( \begin{array}{ccc} C_1 \\ C_2 \end{array} \right)
\\ & = e^{t} \left( \begin{array}{ccc} C_1 (2 \cos t + \sin t) + C_2 ( 2 \sin t - \cos t)  \\ - C_1 \cos t - C_2 \sin t \end{array} \right)
\end{align*} \]となるので、一般解を\[
\left\{ \begin{array}{l} x = C_1 e^{t} (2 \cos t + \sin t) + C_2 e^{t} ( 2 \sin t - \cos t) \\ y = - C_1 e^{t} \cos t - C_2 e^{t} \sin t \end{array}\right.
\]と求めることができる。

(3)

\( P \) の逆行列 \( P^{-1} \) は\[
P^{-1} =  \left( \begin{array}{ccc} 0 & -1 \\ -1 & -2 \end{array} \right)
\]となる。

よって、\[\begin{align*}
e^{tA} & = P e^{tD} P^{-1}
\\ & = \left( \begin{array}{ccc} 2 & -1 \\ -1 & 0 \end{array} \right) \cdot e^{t} \left( \begin{array}{ccc} \cos t & \sin t \\ - \sin t & \cos t \end{array} \right) \left( \begin{array}{ccc} 0 & -1 \\ -1 & -2 \end{array} \right)
\\ & = e^{t} \left( \begin{array}{ccc} 2 \cos t + \sin t & 2 \sin t - \cos t \\ - \cos t & - \sin t \end{array} \right)  \left( \begin{array}{ccc} 0 & -1 \\ -1 & -2 \end{array} \right)
\\ & = e^{t} \left( \begin{array}{ccc} -2 \sin t + \cos t & -5 \sin t \\ \sin t & \cos t + 2 \sin t  \end{array} \right)
\end{align*}\]と計算できる。

５．非同次の連立微分方程式の解き方（おまけ）

\[
\left\{ \begin{array}{l} \frac{dx}{dt} = x + 2y + e^{2t} \\ \frac{dy}{dt} = 2x + y + 2e^{2t} \end{array}\right.
\]のような非同次の連立微分方程式も、\[
\vec{b} = \left( \begin{array}{ccc}  e^{2t} \\ e^{2t}  \end{array} \right)
\]とすることで、\[
\frac{d \vec{x} }{dt}   = A \vec{x} + \vec{b} (t) \tag{1}
\]のように行列を用いてとくことができます。

ここで、同次形\[
\frac{d \vec{x} }{dt}   = A \vec{x}
\]の一般解は任意定数ベクトル \( \vec{c} \) を用いて\[
\vec{x} = e^{tA} \vec{c}
\]と表せるのでしたね。

ここで、任意定数ベクトル \( \vec{c} \) が何かしらの \( t \) の関数 \( \vec{c} (t) \) ではないかと考えます。おなじみの定数変化法ですね。

（以下、\( \vec{c} (t) \) を \( \vec{c} \) と表記します。）

ここで、\[
\vec{x} = e^{tA} \vec{c}
\]を \( t \) で微分すると、\[
\frac{d \vec{x} }{dt}   = A e^{tA} \vec{c} + e^{tA} \frac{d \vec{c}}{dt}
\]となりますね。

これを与えられた式(1)に代入すると、\[\begin{align*}
\color{red}{A e^{tA} \vec{c}} + e^{tA} \frac{d \vec{c}}{dt} & = A \vec{x} + \vec{b}
\\ & = \color{red}{Ae^{tA} \vec{c}} + \vec{b}(t)
\end{align*}\]となるので、\[
e^{tA} \frac{d \vec{c}}{dt} = \vec{b}(t) \]\[
\frac{d \vec{c}}{dt} = e^{-tA} \vec{b}(t)
\]と変形することで、ベクトル \( \vec{c}(t) \) を任意定数が新たな入ったベクトル \( \vec{C} \) を用いて\[
\vec{c} = e^{-tA} \vec{b}(t) \ dt + \vec{C}
\]で計算することができます。

よって非同次形の連立微分方程式\[
\frac{d \vec{x} }{dt}   = A \vec{x} + \vec{b} (t)
\]の一般解は\[\begin{align*}
\vec{x} & = e^{tA} \vec{c}
\\ & = e^{tA} \left( \int e^{-tA} \vec{b}(t) \ dt + \vec{C} \right)
\end{align*}\]で求めることができます。

軽く例題で計算過程の確認をしておきましょう。

例題6

連立微分方程式\[
\left\{ \begin{array}{l} \frac{dx}{dt} = x + 2y + e^{2t} \\ \frac{dy}{dt} = 2x + y + e^{2t} \end{array}\right.
\]は、行列を用いて\[
\frac{d}{dt} \left( \begin{array}{ccc} x \\ y \end{array} \right) = \left( \begin{array}{ccc} 1 & 2 \\ 2 & 1 \end{array} \right) \left( \begin{array}{ccc} x \\ y \end{array} \right) + \left( \begin{array}{ccc}  e^{2t} \\ 2 e^{2t}  \end{array} \right)  \]\[
\frac{d \vec{x} }{dt} = A \vec{x} + \vec{b}
\]と表される。

このときの与えられた連立微分方程式の特殊解を1つ求めなさい。

ただし、必要であれば\[
e^{tA} = \frac{1}{2} \left( \begin{array}{ccc} e^{-t} + e^{3t} & -e^{-t} + e^{3t} \\ -e^{-t} + e^{3t} & e^{-t} + e^{3t} \end{array} \right)
\]を用いてもよい。

解説6

特殊解の1つは\[
e^{tA} \int e^{-tA} \vec{b}(t) \ dt
\]と求めることができる。（導出仮定省略）

\[
e^{-tA} = \frac{1}{2} \left( \begin{array}{ccc} e^{t} + e^{-3t} & -e^{t} + e^{-3t} \\ -e^{t} + e^{-3t} & e^{t} + e^{-3t} \end{array} \right)
\]となる。

また、\[\begin{align*}
e^{-tA} \vec{b} & = \frac{1}{2} \left( \begin{array}{ccc} e^{t} + e^{-3t} & -e^{t} + e^{-3t} \\ -e^{t} + e^{-3t} & e^{t} + e^{-3t} \end{array} \right) \left( \begin{array}{ccc} e^{2t} \\ e^{2t} \end{array} \right)
\\ & = \left( \begin{array}{ccc} e^{-t} \\ e^{-t} \end{array} \right)
\end{align*}\]となるので、\[\begin{align*}
\int e^{-tA} \vec{b} \ dt & = \int \left( \begin{array}{ccc} e^{-t} \\ e^{-t} \end{array} \right) \ dt
\\ & =  \left( \begin{array}{ccc} \int e^{-t} \ dt \\ \int e^{-t} \ dt \end{array} \right)
\\ & =  \left( \begin{array}{ccc} - e^{-t} \\ - e^{-t} \end{array} \right)
\end{align*}\]と計算できます。

（特殊解の1つを出すので任意定数を省略しています。）

よって、特殊解の1つは、\[\begin{align*}
\vec{x} & =  e^{tA} \int e^{-tA} \vec{b}(t) \ dt
\\ & = \frac{1}{2} e^{-tA} \left( \begin{array}{ccc} e^{t} + e^{-3t} & -e^{t} + e^{-3t} \\ -e^{t} + e^{-3t} & e^{t} + e^{-3t} \end{array} \right) \left( \begin{array}{ccc} - e^{-t} \\ - e^{-t} \end{array} \right)
\\ & = \left( \begin{array}{ccc} e^{-2t} \\ - e^{2t} \end{array} \right)
\\ & = \left( \begin{array}{ccc} x \\ y \end{array} \right)
\end{align*}\]となるので、\[
\left\{ \begin{array}{l} x = - e^{2t} \\ y = - e^{2t} \end{array}\right.
\]となります。

なお、非同次の2元連立微分方程式を行列を用いて解くのは計算量がかなり多くなってしまうため、あまりおすすめできません。

（非同次の2元連立微分方程式であれば、2次の微分方程式にしてから解くのがおすすめです。）

６．練習問題

では、実際に

• 対角化を用いて連立微分方程式を解く
• 指数行列の仕組みと導出
• 指数行列を用いて連立微分方程式を解く

練習をしてみましょう。

今回は、記事の分量の都合上、練習問題は別の記事にしております。

練習問題にチャレンジしたい人は下の記事をぜひご覧ください。

www.momoyama-usagi.com

７．さいごに

かなり長い記事になってしまいましたが今回は、

• 対角化を用いて連立微分方程式を解く方法
• 指数行列の仕組みと導出方法
• 指数行列を用いて連立微分方程式を解く方法

について紹介しました。

対角化を用いて連立微分方程式を解く方法については期末試験でもよく出てくるので確実に復習しておきましょう。

指数行列については、仕組みをなんとなくで理解していただけたらOKです。

（おそらく期末試験には出ないと思うので…　院試なら必要かも。）

次回は、実際に対角化や指数行列を用いた連立微分方程式を解いたり、指数行列を求める計算演習問題を用意する予定です。