条件付き確率・ベイズの定理について

こんにちは、ももやまです。

今日は「条件付き確率」と条件付き確率を応用した「ベイズの定理」についてわかりやすくまとめました！

 

 

「確率ってなんだっけ～」、とか「確率の求め方忘れっちゃった～」と不安な人向けのために、1時間で「確率」を復習できる記事を用意しています。

確率の知識に不安な方、確率の確認をしておきたい人はぜひこちらの記事をお読みください。

www.momoyama-usagi.com

スポンサードリンク

１．条件付き確率

とある事象 \( A,B \) があるとします。ある事象 \( A \) が起こったときの事象 \( B \) が起こる確率のことを条件付き確率といいます。

記号で表すと \( P(B|A) \) と書けます。記号で書く場合は \( A,B \) の順番が逆になっているので注意してください*1。

 

条件付き確率は、表やベン図を書くとわかりやすいです。

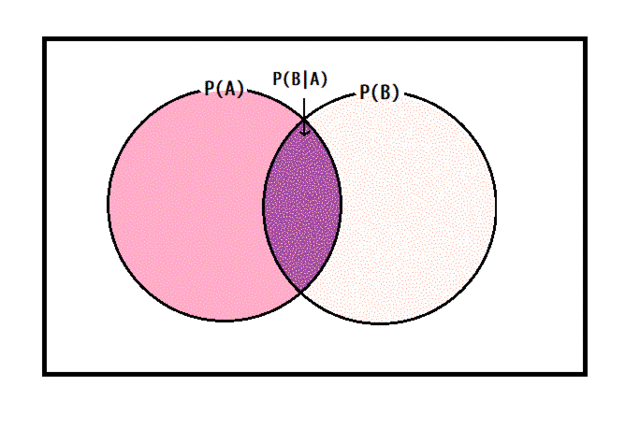
まずはベン図で表してみます。

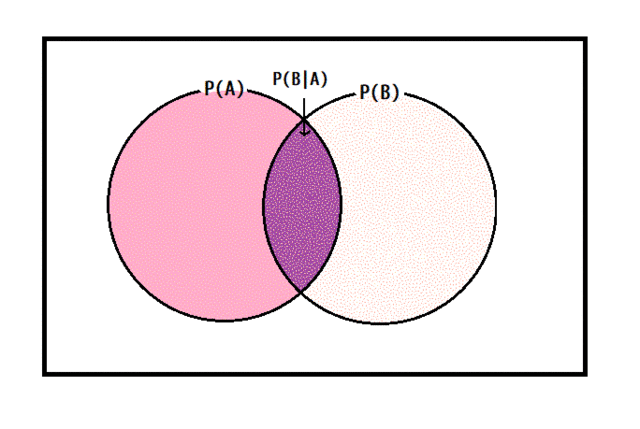事象 \( A \) が起こった場所をピンク色で表しています。ピンク色の中で、事象 \( B \) が含まれている部分が \( P(B|A) \) となり、紫色で表しています。

 

つぎに表を書いてみます。私の個人的おすすめはベン図よりも表です。

	A○	A×	A合計
B○	15	5	20
B×	10	20	30
B合計	25	25	50

 

この表から、様々な確率を読み取ることができます。

 

例えば、事象 \( P(A) \) が起こる確率は、ピンク色の部分。
事象 \( P(B) \) が起こる確率は水色の部分になることがわかりますね。

 

では、ある事象 \( A \) が起こったときの事象 \( B \) が起こる条件付き確率 \( P(B|A) \) を表から読み取って解いていきましょう。

 

まず、ある事象 \( A \) が起こったとき(A○)の事象 \( B \) が起こるか起こらないかは、表の次の色を塗った部分で確認することができます。 

	A○	A×	A合計
B○	15	5	20
B×	10	20	30
B合計	25	25	50

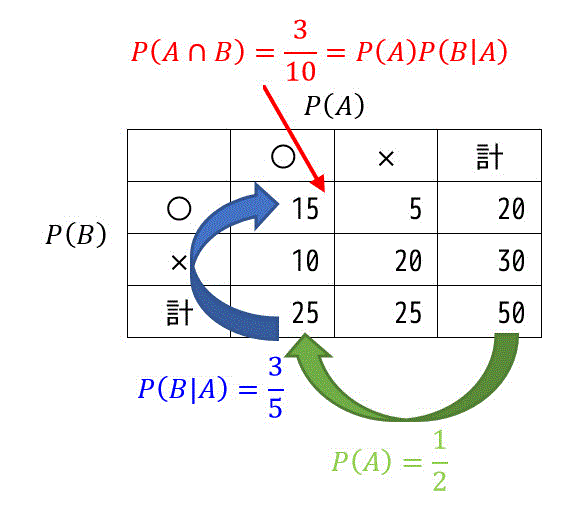
 表より事象 \( A \) が起こる確率は25回なのがわかりますね。25回の中で、Aが起こるのは15回、Aが起こらないのは10回なのがわかります。つまり、条件付き確率 \( P(B|A) \) は、\[ P(B|A) = \frac{3}{5} \]になることがわかります。

 

事象 \( A \) と事象 \( B \) がともに起こる確率 \( P ( A\cap B) \) は、表より \( 3/10 \) と読み取る事ができますね。条件付き確率 \( P(B|A) \) は、以下の公式で求めることができます。\[ P(B|A) = \frac{P(A \cap B)}{P(A)}\]

 

実際に \( P(B|A) \) を公式に代入して計算してみましょう。\( P(A) = 25/50 = 1/2 \) なので、\[ P(B|A) = \frac{P(A \cap B)}{P(A)} = \frac{ \frac{3}{10} }{ \frac{1}{2} } = \frac{3}{5} \]と求められます。

 

表で確かめてみましょう。上の式を変形すると、\[P(A \cap B) = P(A)P(B|A)\]が導出できます。確かに上で計算した場合と表で読み取った場合両方とも同じ確率になっていますね。

 

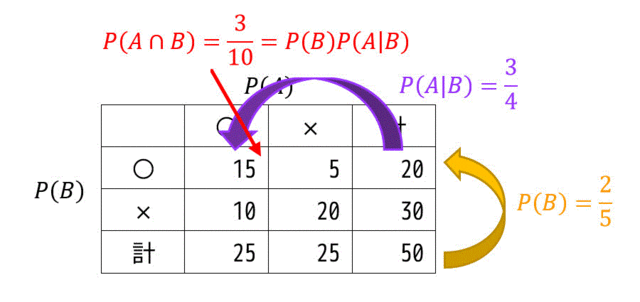
同様に、ある事象 \( B \) が起こったときの事象 \( A \) が起こる条件付き確率 \( P(A|B) \) も表で確かめてみましょう。

スポンサードリンク

２．ベイズの定理

ある事象 \( A \) が起こったときの事象 \( B \) が起こる条件付き確率 \( P(B|A) \) から、ある事象 \( B \) が起こったときの事象 \( A \) が起こる条件付き確率 \( P(A|B) \) を求める式をベイズの定理といいます。

 

さきほど上の例で \( P(A|B) \) を使った場合、 \( P(B|A) \) を使った場合の2つの方法で \( P(A \cap B) \) をもとめましたね。

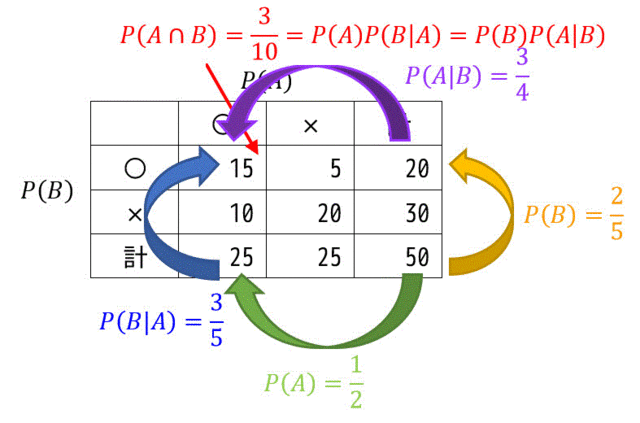
この２つの式を使うと、\(  P(A)P(B|A) = P(B)P(A|B) \) という式が得られます。この式を変形すると、\[P(B|A) = \frac{P(A|B)P(B)}{P(A)}\]となり、これがベイズの定理となります*2。

 

ベイズの定理は、この公式を丸覚えするのではなく、なぜこの式になるかを導けるようにしておくのがいいと思います！

スポンサードリンク

３．練習問題

では、２問ほど練習してみましょう！

練習1

お菓子をきのこの山かたけのこの里を判定する機械がある。

この機械は、

• たけのこの里の \( \frac{24}{25} \) は正しくたけのこの里と判定
• きのこの山の \( \frac{3}{50} \) を間違えてたけのこの里と判定

する。

• 無作為に選んだお菓子がたけのこの里である事象を \( A \)
• 無作為に選んだお菓子がきのこの山である事象を \( B \)
• 無作為に選んだお菓子が機械によりたけのこの里と判定される事象を \( C \)

とし、同じ数のきのこの山とたけのこの里を判別（ \( P(A) = P(B) = 1/2 \) ）するとき、以下の問いに答えなさい。

 

(1) 無作為に選んだお菓子が「たけのこの里」であり、かつそれが正しく「たけのこの里」判定されている確率 \( P(A \cap C) \) および無作為に選んだお菓子が「きのこの山」であり、かつそれが誤って「たけのこの里」と判定されている確率 \( P(B \cap C) \) を求めなさい。

(2) 無作為に選んだお菓子が機械によりたけのこの里と判定される確率 \( P(C) \) を求めなさい。

(3) 無作為に選んだお菓子が機械によりたけのこの里と判定されたとき、そのお菓子が正しくたけのこの里に分類されている条件付き確率 \( P(A|C) \) を求めなさい。

 

解答1

表を書くとわかりやすくなります。今回は全体を100 [%] とした表で解いています。

(1)

無作為にたけのこの里を選ぶ確率は \( 1/2 \)、たけのこの里の \( 24/25 \) は正しくたけのこの里と判定されるため、\( P(A \cap C) \) は\[ P(A \cap C) = \frac{1}{2} \times \frac{24}{25} = \frac{12}{25} \]となる。

また、無作為に選んだお菓子が「きのこの山」であり、かつそれが誤って「たけのこの里」と判定されている確率 \( P(B \cap C) \) は、\[ P(B \cap C) = \frac{1}{2} \times \frac{3}{50} = \frac{3}{100} \]となる。

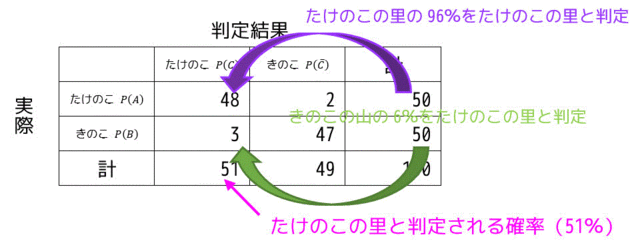
(2)

あるお菓子がたけのこの里と判定される確率 \( P(C) \) は、 \( P(A \cap C) \) と \( P(B \cap C) \) の和で求められる。

よって、\[ P(A \cap C) = \frac{12}{25} + \frac{3}{100} = \frac{51}{100} \]となる。

 

(3) 

条件付き確率 \( P(A|C) \) は、以下のように求められる。\[ P(A|C) = \frac{P(A \cap C)}{P(C)} = \frac{ \frac{12}{25} }{ \frac{51}{100} } = \frac{12}{25} \cdot \frac{100}{51} = \frac{48}{51} = \frac{16}{17}\]

 

条件付き確率がわからなくなってしまったときは、下のように表を書いてみるとわかりやすくなります。

このような条件付き確率は再現率・適合率を求める際にも使います。

 

再現率は、実際に該当するものからどれだけ機械や検査などで判定することができる確率、適合率は、検査結果で該当したものが実際にどれだけ該当しているかを表します。

 

今回の例でいうと、再現率はたけのこの里の中から機械でどれだけたけのこの里を見つけることができたか、つまり \(  P(A|C) \) に該当します。また、適合率は、機械がたけのこの里と判定したものの中から実際にたけのこの里であったのはどれくらいあるのか、つまり \(  P(C|A) \) を表します。

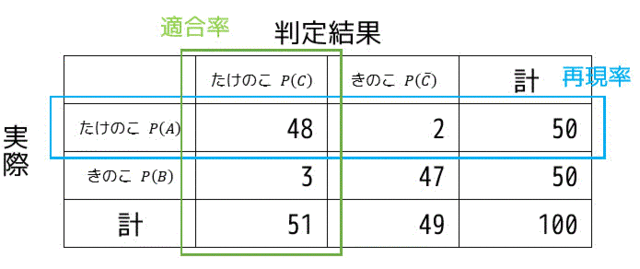
今回の場合だと、\[ (再現率) = \frac{24}{25} \ \  \ \ \  (適合率) = \frac{16}{17}\]となりますね。

 

再現率、適合率に関してはこちらのブログにまとめているのでぜひご覧ください！

www.momoyama-usagi.com

 

練習2

4つの機械 A,B,C,D がある。それぞれの機械の生産量の比は 4:3:2:1 である。つまり、\( P(A) = 0.4 \), \( P(B) = 0.3 \), \( P(C) = 0.2 \), \( P(D) = 0.1 \) である。また、不良品Eの出る割合は2%, 3%, 4%, 5% である。つまり、\( P(E|A) = 0.02 \), \( P(E|B) = 0.03 \), \( P(E|C) = 0.04 \), \( P(E|D) = 0.05 \) である。

 

このとき、次の問いに答えなさい。

 

(1) ある製品がAで生産され、かつ不良品である確率 \( P(A \cap E) \) を求めなさい。
(2) ある製品が不良品である確率を求めなさい。
(3) ある製品が不良品だった場合に、それがAで生産されたものである確率を求めなさい。
(4) ある製品が不良品だった場合、それはどの機械で生産されたものと考えるのがよいか。結論とその理由を答えなさい。
(5) ある製品が不良品ではなかった場合、それはどの機械で生産されたものと考えるのがよいか。結論とその理由を答えなさい。

解答2

こちらも、わからなくなったら表を書いてみましょう。

表を書くことでかなりわかりすくなります。

 

(1) 
\( P(A \cap E) \) は、Aが生産される確率 \( P(A) \) と、Aの中で不良品が発生する条件付き確率 \( P(E|A) \) の積で求められる。\[ P(A \cap E) = 0.4 \cdot 0.02 = 0.008 =\frac{8}{1000} = \frac{1}{125}\]と求められる。

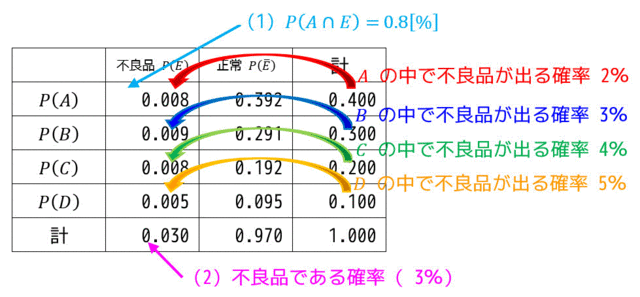
(2)

ある製品が不良品である確率は、製品A,B,C,Dが生産され、かつ不良品である確率をすべて足した和となる。\[ P(B \cap E) = 0.3 \cdot 0.03 = 0.009 =\frac{9}{1000}\] \[ P(C \cap E) = 0.2 \cdot 0.04 = 0.008 =\frac{8}{1000}\] \[ P(D \cap E) = 0.1 \cdot 0.05 = 0.005 = \frac{5}{1000}\]となる。よってある製品が不良品である確率は、\[\frac{8}{1000} + \frac{9}{1000} + \frac{8}{1000} +  \frac{5}{1000} = \frac{30}{1000} = \frac{3}{100} \]となる。

(3)

ある製品が不良品だった場合に、それがAで生産されたものである条件付き確率 \( P(A|E) \) は、\[P(A|E) = \frac{P(A \cap E)}{P(E)} = \frac{ \frac{1}{125} }{ \frac{3}{100} } = \frac{8}{30} = \frac{4}{15}\]と求められる。

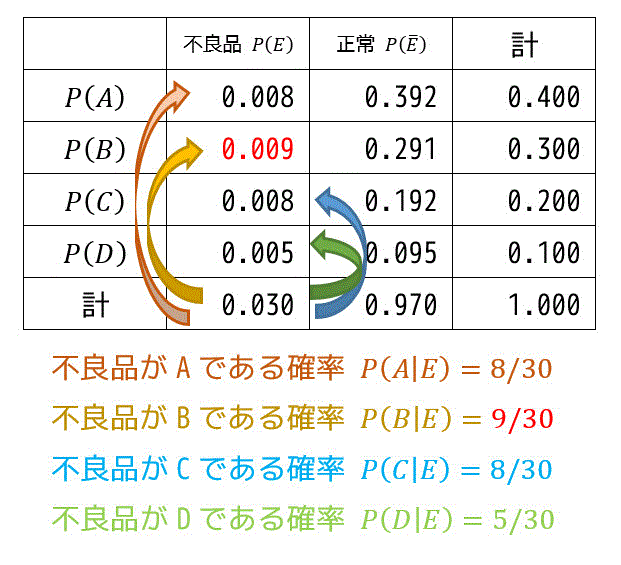
(4)

(3)と同様にB,C,Dが不良品だった場合の条件付き確率を求めていく*3。
\[P(B|E) = \frac{P(B \cap E)}{P(E)} = \frac{ \frac{9}{1000} }{ \frac{3}{100} } = \frac{9}{30}\] \[P(C|E) = \frac{P(B \cap E)}{P(E)} = \frac{ \frac{9}{1000} }{ \frac{3}{100} } = \frac{8}{30}\] \[P(D|E) = \frac{P(B \cap E)}{P(E)} = \frac{ \frac{9}{1000} }{ \frac{3}{100} } = \frac{5}{30}\]この4つの確率を比べると、不良品だった場合にBで生産されたものである条件つき確率が一番大きいことがわかる。よって答えはB。

(5)

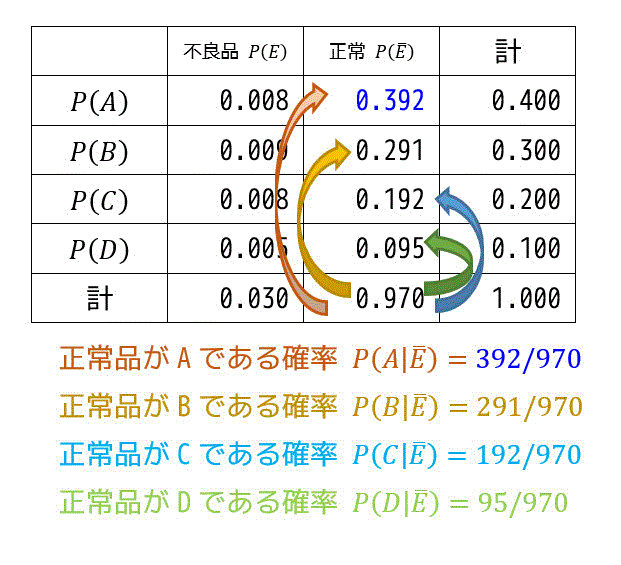
ある製品がA,B,C,Dで生産され、かつ不良品でない確率 \( P(A \cap \bar{E}) \), \( P(B \cap \bar{E}) \), \( P(C \cap \bar{E}) \), \( P(D \cap \bar{E}) \) を求める*4。

 

\[ P(A \cap \bar{E}) = 0.4 \cdot (1.00-0.02) = 0.392 = \frac{392}{1000}\] \[ P(B \cap \bar{E}) = 0.3 \cdot (1.00-0.03) = 0.291 = \frac{291}{1000}\] \[ P(C \cap \bar{E}) = 0.2 \cdot (1.00-0.04) = 0.192 = \frac{192}{1000}\]  \[ P(D \cap \bar{E}) = 0.1 \cdot (1.00-0.05) = 0.095 = \frac{95}{1000}\]となる。

 

これをある製品が不良品でない確率で割ればよい。不良品ではない確率はA,B,C,Dどれも同じなので不良品ではなかった場合はAで生産されたものと考えるのがよい*5。

 

 

５．まとめ

今回は条件付き確率、ベイズの定理についてまとめました。

ベイズの定理は大学の確率・統計で習うところが多いと思いますが、内容自体は高校生でも十分に理解できるような内容なのでぜひ理解しましょう！