スポンサードリンク
こんにちは、ももやまです。
突然ですが問題です!
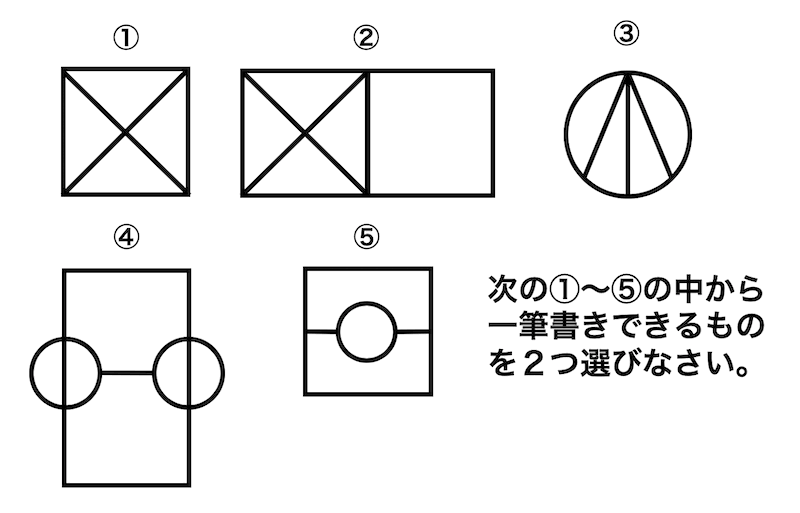
つぎの①〜⑤の中から一筆書きできるものを2つ選んでみましょう。
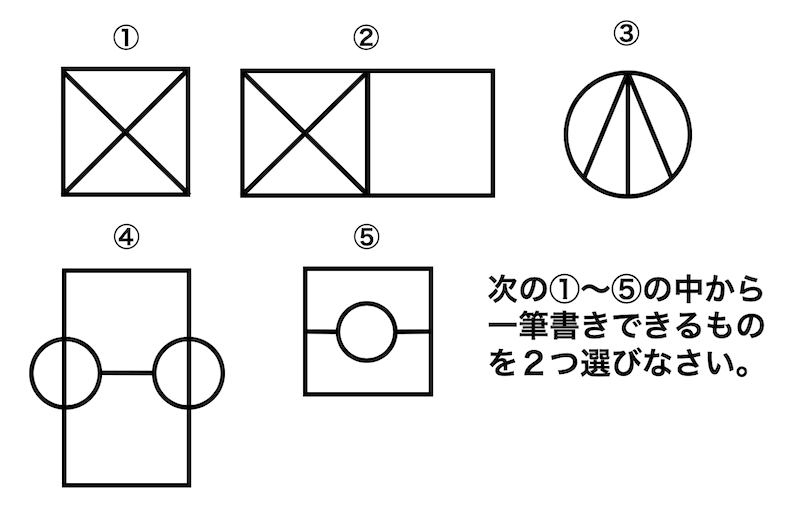
引用元:パズル算数クイズ
(解答は2の例題2の解説に書いています。)
今回は一筆書きができるかどうかの判定方法をメインにまとめていきたいと思います。
(一筆書きの判定法は2章にまとめています。)
また、グラフ理論で習うオイラーグラフ・ハミルトングラフとはどんなグラフか、どうやったら判定ができるかについてもまとめています。
前回のグラフ理論の記事(第9羽)はこちら!
(グラフ理論における基本用語のまとめです。)
目次
スポンサードリンク
1.オイラーグラフ
(1) オイラー回路・オイラーグラフとは
あるグラフにおいて一筆書き(すべての辺を1度だけ通るようなたどり方)ができてかつ書き始めの点と書き終わりの点が同じ回路(経路のこと)のことをオイラー回路と呼びます。
また、オイラー回路を持つようなグラフ、つまり一筆書きができてかつ書き始めの点に戻ってこれるようなグラフのことをオイラーグラフと呼びます。
まずは実際にオイラーグラフかどうかを地道にたどりながら確認していきましょう。
例題1
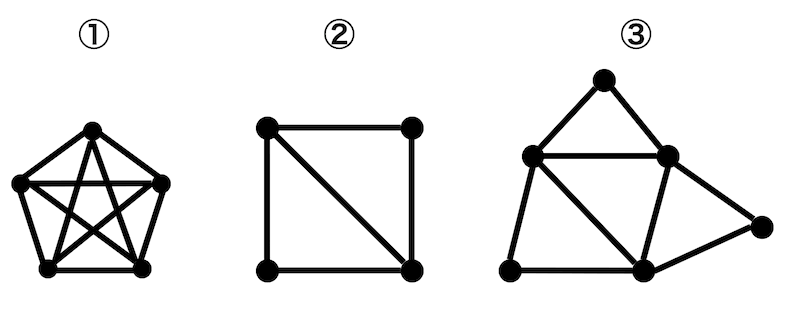
次の①~③の中から、オイラーグラフとなるものを選びなさい。
解答1
経路をたどってみましょう。
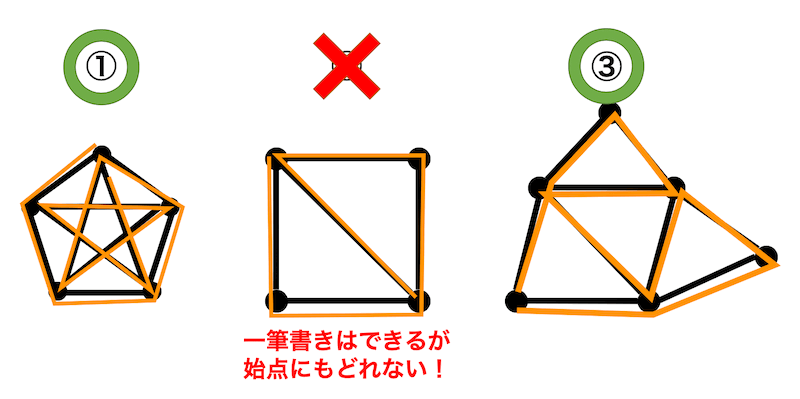
すると、①と③は一筆書きができてかつ始点に戻ってこれるので一筆書きの経路(オイラー回路)を持ちますね。
しかし、②は一筆書きはできるのですがどうがんばっても始点に戻ることができません。なのでオイラー回路とはいえませんね。
(2) オイラーグラフかどうかの簡単な判別法
オイラーグラフの判定は簡単に行うことができます。
先程例題で出した3つのグラフの次数(つながっている辺の数)を確認してみましょう。
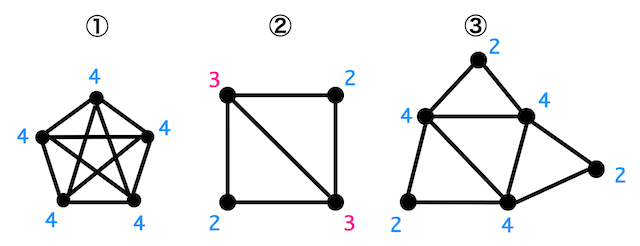
オイラーグラフである①と③の頂点の次数は全部偶数となっていますね。
実はこれは偶然ではなく、オイラーグラフの条件となっているのです。
つまり、あるグラフがオイラーグラフ(一筆書きして元に戻ってこれるようなグラフ)であるための条件は、すべての頂点の次数が偶数であることと言い換えることができますね*1。
[簡単な理由(証明ほどではない)]
始点(終点)の点とそれ以外の点に場合分けを考えます。
始点以外の点は、必ず点を通過する前に次数が+1、通過後に次数が+1されるので点を通過するたびに次数は+2されますね。なので始点以外の点は必ず次数が偶数となりますね。
また、始点に関してもスタート次に+1、ゴール次に+1され合計+2されるので始点も必ず次数が偶数となります。
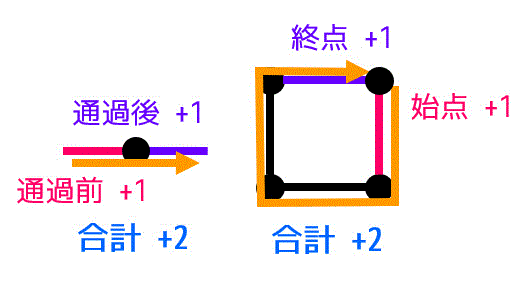
よって、すべての頂点の次数が偶数であれば必ずオイラーグラフとなるのです!
グラフ \( G \) の次数がすべて偶数であれば、グラフ \( G \) は必ずオイラーグラフである。
(3) 有向グラフの場合
有向グラフの場合もやっておきましょう。
例えば、下のようなグラフは一筆書きできてかつ始点に戻ることができますね。(経路は省略します…)
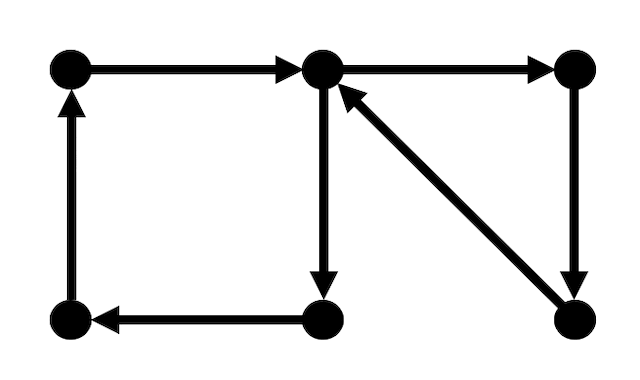
有向グラフの一筆書きができてかつ書き始めの点と書き終わりの点が同じ回路(たどり方こと)のことを有向オイラー回路と呼びます。
有向グラフの場合、有向オイラー回路を持つことがオイラーグラフの条件となります。
有向グラフの場合もオイラーグラフであるかどうかは次数を確認することで判定ができます。しかし、有向グラフの次数は入次数と出次数の2つにわかれていましたね。
ここで少し復習しておきましょう。
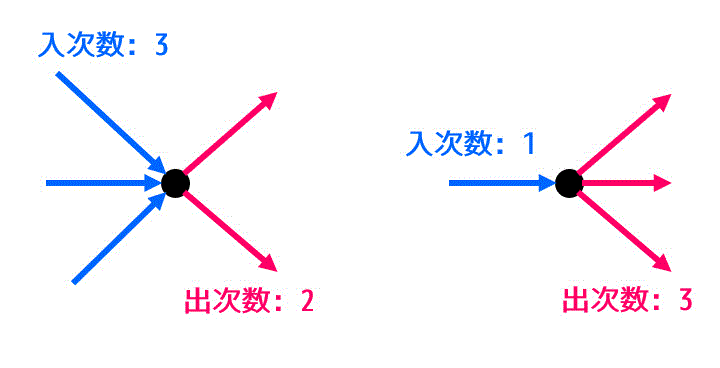
ある点に入ってくる辺の数を表す入次数、ある点から出ていく辺の数を表す出次数と呼ぶのでしたね。
入次数、出次数などグラフ理論の基本用語についてはこちらにまとめているので今までに出た基本用語の中でわからないようなものがあればこちらで確認しましょう。
無向グラフと同じように始点(終点)の点とそれ以外の点に場合分けを考えます。
始点以外の点は、点を通過する前に入次数+1、通貨した後に出次数+1されますね。
また、始点の場合、スタート次に出次数+1、ゴール次に入次数+1されます。
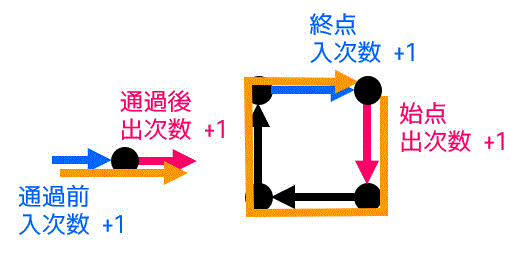
なのでオイラーグラフの場合、入次数と出次数は常に同じになりますね。これが有向グラフの場合のオイラーグラフの条件となります。
有向グラフ \( G \) の入次数と出次数が等しければ有向グラフ \( G \) は必ずオイラーグラフである。
スポンサードリンク
2.一筆書きができるグラフ(半オイラーグラフ)
(1) オイラーグラフかどうかの簡単な判別法
いよいよ本題です。
半オイラーグラフは一筆書きはできるものの、始点に戻ってくることができないようなグラフを表します。
つまり、一筆書きができるグラフは始点に戻れる「オイラーグラフ」と一筆書きができない「半オイラーグラフ」の2つにわかれます。
「半オイラーグラフ」の場合もオイラーグラフのときと同様にそれぞれの頂点における次数を確認するだけで半オイラーグラフかどうかを確認することができます。
始点以外の点は、オイラーグラフと同じく、点を通過する前に次数が+1、通過後に次数が+1され、合計+2されるので次数は必ず偶数となります。
しかし、始点と終点はそれぞれ異なるので始点で次数が+1、始点ではない終点で次数が+1されるので始点と終点だけは次数は奇数となります。
つまり、次数が奇数の点(奇点)が2つであれば半オイラーグラフとなるのです!
グラフ \( G \) の次数が奇数の点(奇点)が2つのとき、グラフ \( G \) は必ず半オイラーグラフである。
(一筆書きの始点は必ずどちらかの奇点に、終点は始点ではない奇点となる)
あるグラフが一筆書きできるための条件をまとめると下のようになります。
あるグラフが一筆書きできるかどうかを判定するときは、それぞれのグラフの次数が奇数の点(奇点)を数えればよい。
奇点が0個 → 一筆書きができ、かつ始点に戻ってくることができる
(どこを始点にしても一筆書きができます。オイラーグラフに相当)
奇点が2個 → 一筆書きができ、かつ始点に戻ってくることができない
(始点はどちらかの奇点、終点は始点ではない奇点となります。半オイラーグラフに相当)
一筆書きの条件
では、最初に出したあの一筆書き問題を解説していきましょう。
例題2
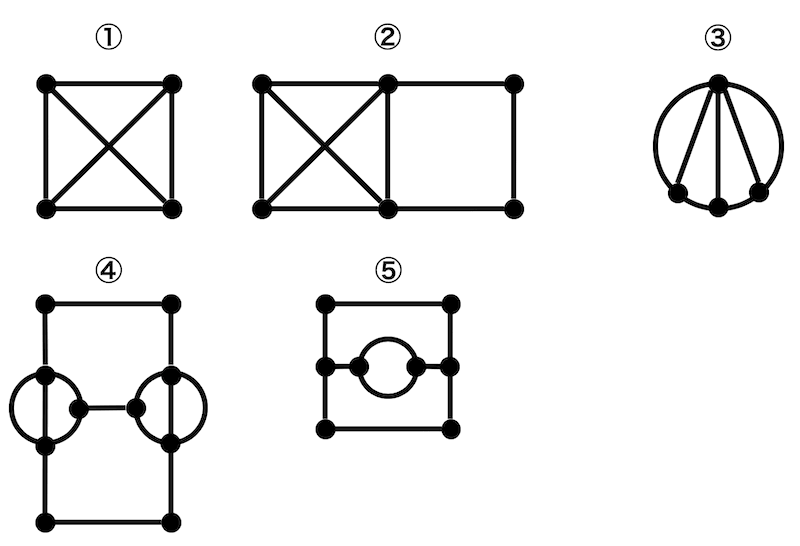
次の①~⑤の中から、一筆書きできるグラフを2つ見つけ、番号で答えなさい。
また、その2つが「オイラーグラフ」・「半オイラーグラフ」のどちらであるかを答えなさい。

解説2
解答:②・④(どちらも半オイラーグラフ)
まずは、それぞれの交点の次数を書いてみましょう*2。
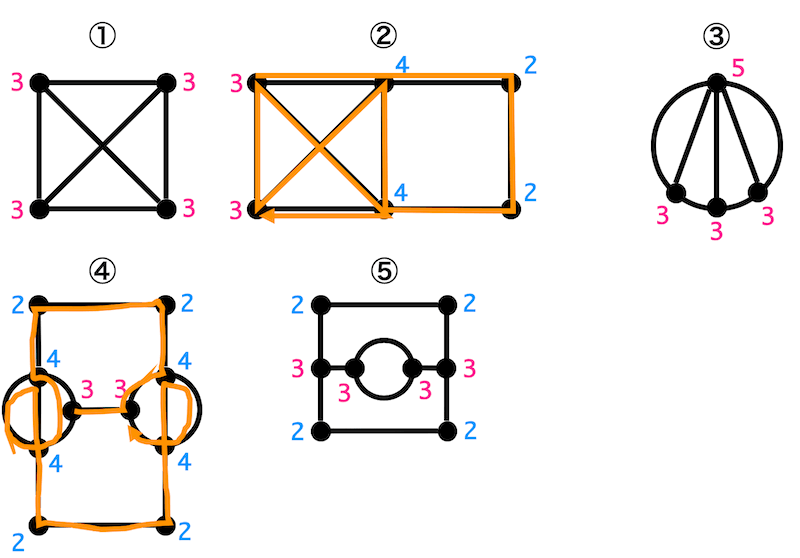
すると、②と④の奇点は2つとなりますね。
なので②と④は一筆書きができることがわかります。(オレンジ色の線は一筆書きのたどり方を表します。)
スポンサードリンク
3.ハミルトングラフ
(1) ハミルトングラフとは
すべての点を1度だけたどって元に戻れるようなたどり方があるようなグラフのことをハミルトングラフと呼びます。
(すべての点を1度だけ通って元に戻れるようなたどり方のことをハミルトン閉路と呼びます。つまり、ハミルトングラフはハミルトン閉路を持つようなグラフを表します。)
例題1で用意した3つのグラフを例に説明しましょう。

この3つのグラフは、下のようにたどることでそれぞれの点を1度だけたどることができますね。
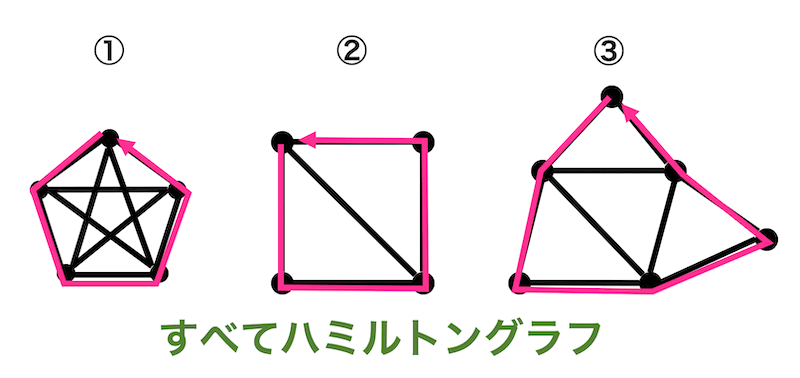
なので3つともハミルトングラフとなります!
1つハミルトングラフかどうかを確認する問題を出しましょう。
例題3
例題2のグラフ①~⑤の中で、ハミルトングラフとなるものは何個ありますか。
解説3
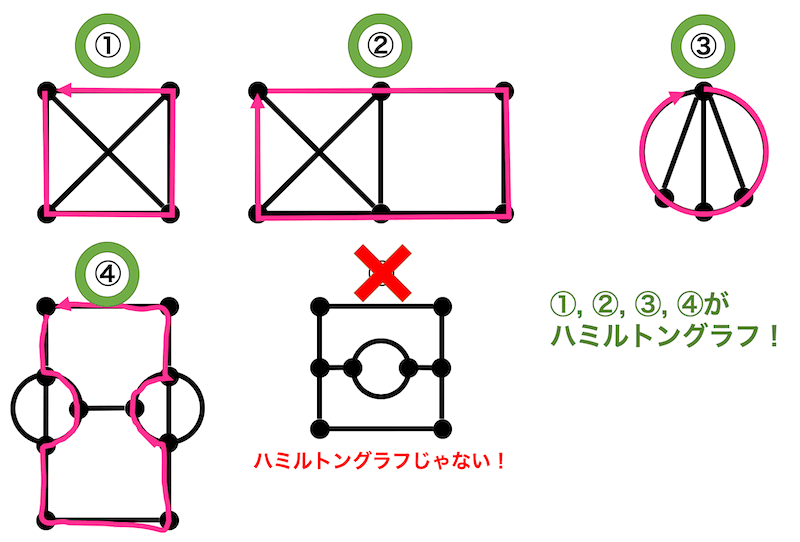
解答:4つ
⑤以外は下のようにたどるとすべての点を1度ずつたどることができるのでハミルトングラフとなります。
(2) ハミルトングラフかどうかの判別法
オイラーグラフの場合は次数に注目することで簡単にオイラーグラフかどうかを判定することができましたね。
しかし、あるグラフがハミルトングラフかどうかを確実に判定する方法は今のところないのです。
もちろんハミルトングラフかどうかを確実にかつ短時間で判定するようなアルゴリズムも現在は存在しません*3。
しかし、確実にハミルトングラフと断言できるための条件は2つあります。
ディラック(Dirac)の定理
ディラックの定理は、すべての点における次数が(頂点数の半分)以上であるグラフはハミルトングラフであるという定理です。
つまり、3つ以上の点があるグラフの点の数 \( n \) がすべての点 \( v \) に対し、\[
d(v) \geqq \frac{1}{2} n
\]を満たせば必ずハミルトングラフであるという定理です。
この定理を少し言い換えて、あるグラフの最小次数 \( d(v)_{min} \) と点の数 \( n \) が\[
2 \cdot d(v)_{min} \geqq n
\]を満たすとき、必ずハミルトングラフであると頭には入れておきましょう。
(あるグラフの最小次数を2倍にしたものが頂点数以上であればハミルトングラフ)
例えば、下の2つのグラフはディラックの定理が成立するので必ずハミルトングラフであると言うことができます。
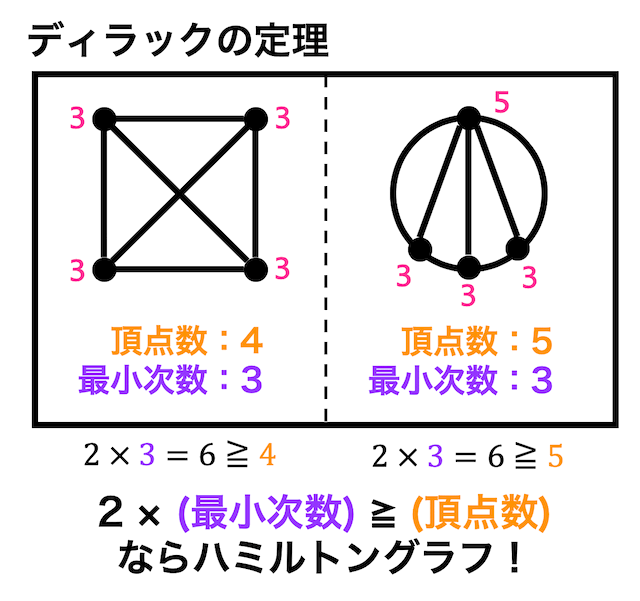
数式で表すと、最小次数 \( d(v)_{min} \)、頂点数 \( n \) に対し\[
2 \cdot d(v)_{min} \geqq n
\]を満たすようなグラフは必ずハミルトングラフとなる。
(ディラックの定理を満たさなくてもハミルトングラフとなるグラフはあるので注意)
オーレ(Ore)の定理
ディラックの定理の条件を少しゆるくしたのがオーレの定理です。俺の定理じゃないですよ。
オーレの定理は、隣接していない任意の2点の次数の合計が頂点数以上であるようなグラフは必ずハミルトングラフとなるという定理です。
つまり、頂点数が \( n \) のグラフの任意の隣接していない2点 \( u \), \( v \) に対し、\[
d(u) + d(v) \geqq n
\]を満たすようなグラフは必ずハミルトングラフとなるような定理です。
実際に定理を適用する際には、隣接していない2点の次数の合計の最小が頂点数以上であるかどうかを確認すればOKです*4。
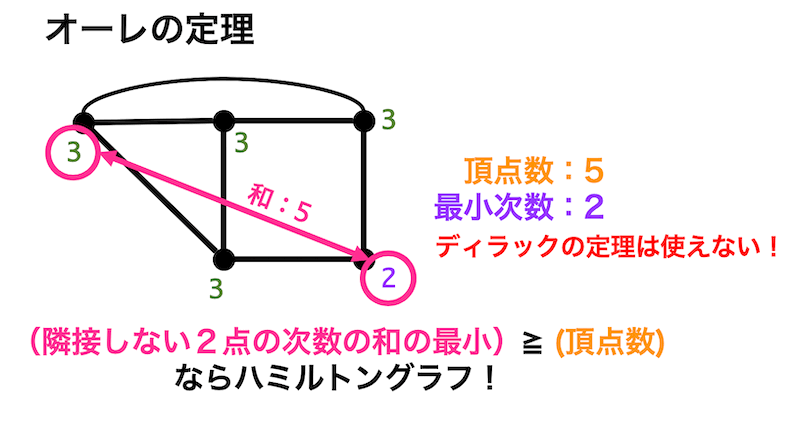
例えば、下のグラフは最小次数は2(2倍すると4)に対し、頂点数は5となってしまうのでディラックの定理は使えません。
しかしオーレの定理を使うと、隣接していない2点の次数の和の最小は5に対し、頂点数も5となるのでハミルトングラフであることを示すことができます。
ちなみにディラックの定理を満たすようなグラフは、必ずオーレの定理も満たします。
(理由)
ディラックの定理を満たすということは、どのグラフも頂点数の半分以上の次数を持っているので、どの2点の次数の和も必ず頂点数以上となる。
よって隣接していない2点の次数の和も当然頂点数以上になるのでオーレの定理も必ず満たす。
4.練習問題
では2問ほど練習してみましょう。
練習1
つぎの(1), (2)の条件を満たすようなグラフを1つ書きなさい。
(1) オイラーグラフであるがハミルトングラフではないグラフ
(2) ハミルトングラフであるがオイラーグラフではないグラフ
(※できれば例題や練習2で使っていないグラフを書きましょう。)
練習2
次の(1)〜(3)の条件を満たすグラフを①〜⑤の中から番号ですべて選びなさい。
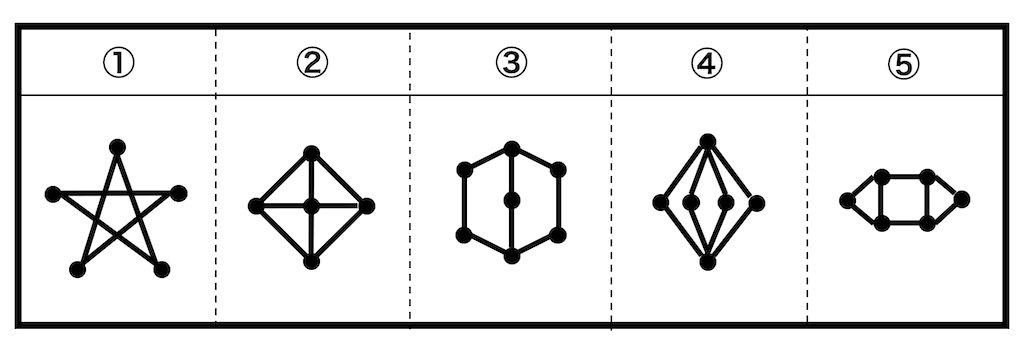
(1) 一筆書きで書けるグラフ
(2) オイラーグラフ
(3) ハミルトングラフ
5.練習問題の答え
解答1
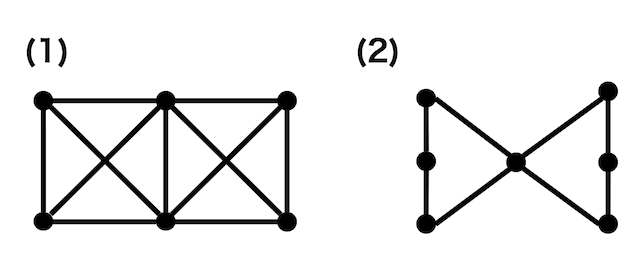
(1) 次数3の点が4つあるのでオイラーグラフではない
(2) どうがんばっても真ん中の次数4の点は2回通過するのでハミルトングラフではない
解答2
解答
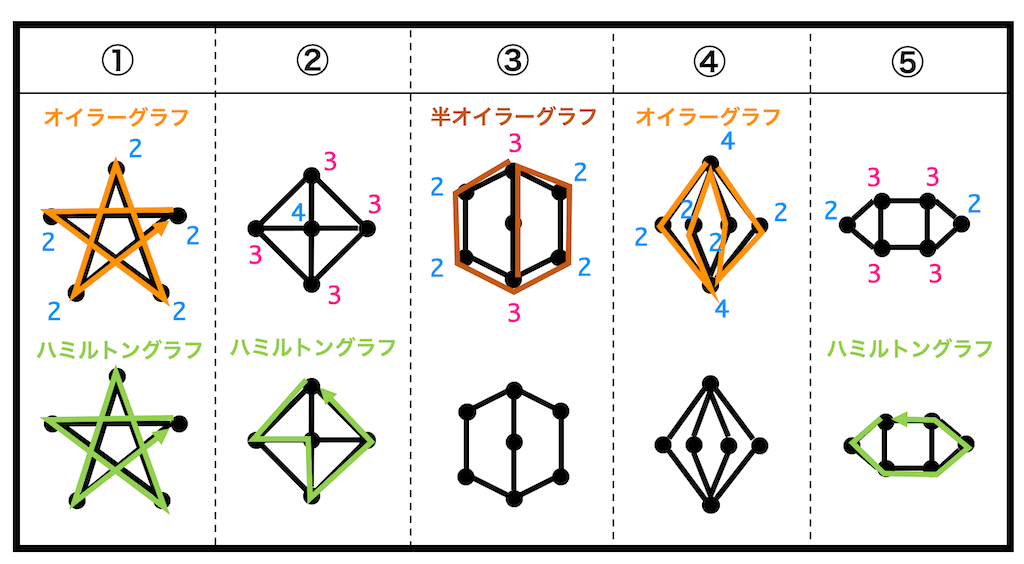
(1) ①・③・④
(2) ①・④
(3) ①・②・⑤
下にオイラーグラフ・半オイラーグラフ・ハミルトングラフの場合のたどり方(オイラー回路、ハミルトン閉路)を示しています。
6.さいごに
今回は一筆書きが可能かの判定方法、およびグラフ理論におけるオイラーグラフ・ハミルトングラフについて解説をしました。
これで一筆書きができるかどうかの判定をゴリ押しせずにすることができますね。
次回はグラフ理論における木構造について解説していきたいとおもいます。
*1:すべての頂点が偶点であること、と参考書には書いてあることがあります。(次数が偶数の点のことを偶点、次数が奇数の点のことを奇点という)
*2:①・②の次数4が省略されていますがご了承ください…。
*3:少しむずかしい言い方をすると、ハミルトングラフかどうかを判定する問題はNP完全問題という世の中にある問題の中でも大変むずかしい部類にあてられています。
NP完全問題について知りたいよって人はこちらの記事をご覧ください。
*4:チェック方法としては、
- 2点の次数の合計の最小を求める
- 2点が隣接していないか確認
(隣接している場合はつぎに2点の次数の合計が小さい組み合わせでチェック) - 2点の合計の最小が頂点数以上かチェック
(頂点数以上ならハミルトングラフ)
とチェックすればOKです。
関連広告・スポンサードリンク